🌕 🌕 🌕 685. 冗余连接 II

难度: 🌕 🌕 🌕

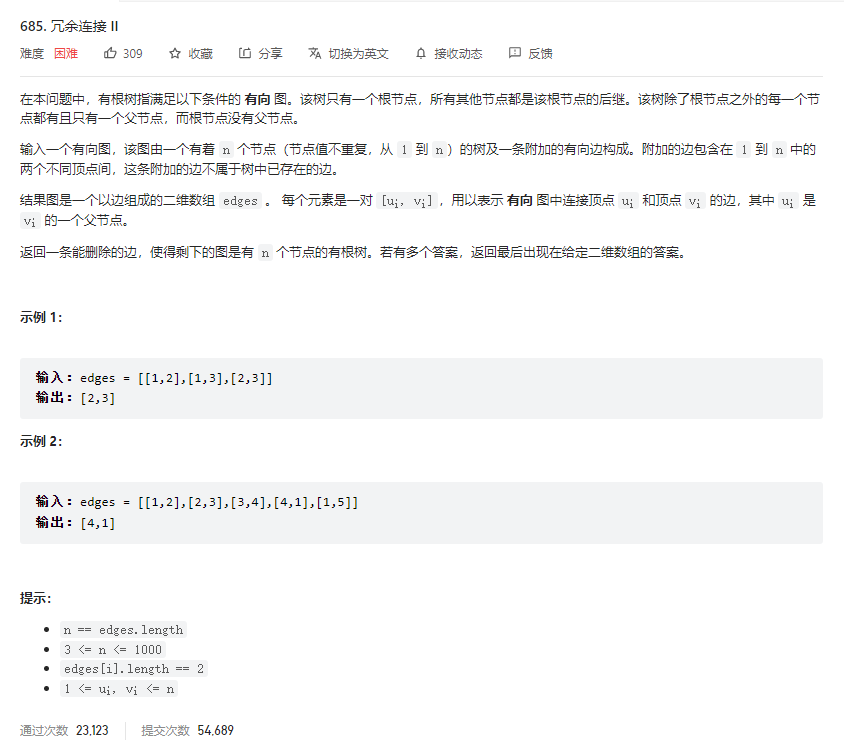
问题描述

---

解法

class Solution {
    int[] parent;
    public int[] findRedundantDirectedConnection(int[][] edges) {
        // 思路：
        // 添加的边只能出现 2 种不同情况：
        // 1. 添加从某个节点指向根节点的边，形成环，此时，需要借助并查集，查看是否有图，如果是图，返回这条边
        // 2. 看树的入度，只有根节点 入度 == 0 其他节点 入度 == 1，看出度无效，因为并没有说是几叉树
        int len = edges.length;
        int[] ins = new int[len + 1]; // 统计各下标处的入度
        int iwant = -1; // 记录哪个 to 的下标处 入度 == 2
        for(int i = 0; i < len; i ++) { // 这里顺序没有关系，反正只是记录 to，之后还要从后往前找 to 对应的边
            int[] array = edges[i];
            int from = array[0];
            int to = array[1];
            ins[to] ++; // 入度 ++
            // System.out.println(Arrays.toString(ins) + "  " + Arrays.toString(array));
            if(ins[to] == 2) {
                // 添加到结果集中，之后尝试删除，看删除哪条有效，这个并不是先出现或后出现的有效，而是要看删除后的效果
                iwant = to;
            }
        }
        if(iwant != -1) {
            // 说明 iwant 作为 to 会出现入度为 2 的情况，从后往前找，是哪条边，尝试删除
            for(int i = len - 1; i >= 0; i --) {
                int[] array = edges[i];
                int to = array[1];
                if(to == iwant) {
                    // 尝试删除
                    if(isValid(edges, len, i)) {
                        return edges[i];
                    }
                }
            }
        }
        // 没有出现入度 == 2 的边，说明出现了环
        // 进行并查集的判断
        // 从后往前遍历，依次尝试删除一条边，若是还出现了环，说明删除该边无用，需要继续尝试下一条，直到删除后不成环
        for(int i = len - 1; i >= 0; i --) {
            if(isValid(edges, len, i)) {
                return edges[i];
            }
        }
        return new int[2];
    }

    private boolean isValid(int[][] edges, int len, int rvIndex) {
        // parent 初始化
        // System.out.println(rvIndex);
        parent = new int[len + 1];
        for(int i = 1; i <= len; i ++) {
            parent[i] = i;
        }
        // 遍历所有边，判断是否能够连接成功
        for(int i = 0; i < len; i ++) {
            // 被删除的边不参与计算
            if(rvIndex == i) {
                continue;
            }
            int[] array = edges[i];
            int from = array[0];
            int to = array[1];
            if(!union(from, to)) {
                // 连接失败，出现图，说明删除该条边无用
                // System.out.println(from + "  " + to);
                return false;
            }
        }
        return true;
    }

    private boolean union(int from, int to) {
        // 找到各自的祖先
        int fatherFrom = getFather(from);
        int fatherTo = getFather(to);
        if(fatherFrom == fatherTo) {
            return false; // 已经连接过，连接失败，出现图
        } else {
            parent[fatherFrom] = fatherTo;
            return true;
        }
    }

    private int getFather(int index) {
        // 递归终止条件
        if(parent[index] == index) {
            return index;
        } else {
            return getFather(parent[index]);
        }
    }
}

---

输出