🌕🌕🌕 218. 天际线问题

难度: 🌕🌕🌕

问题描述

---

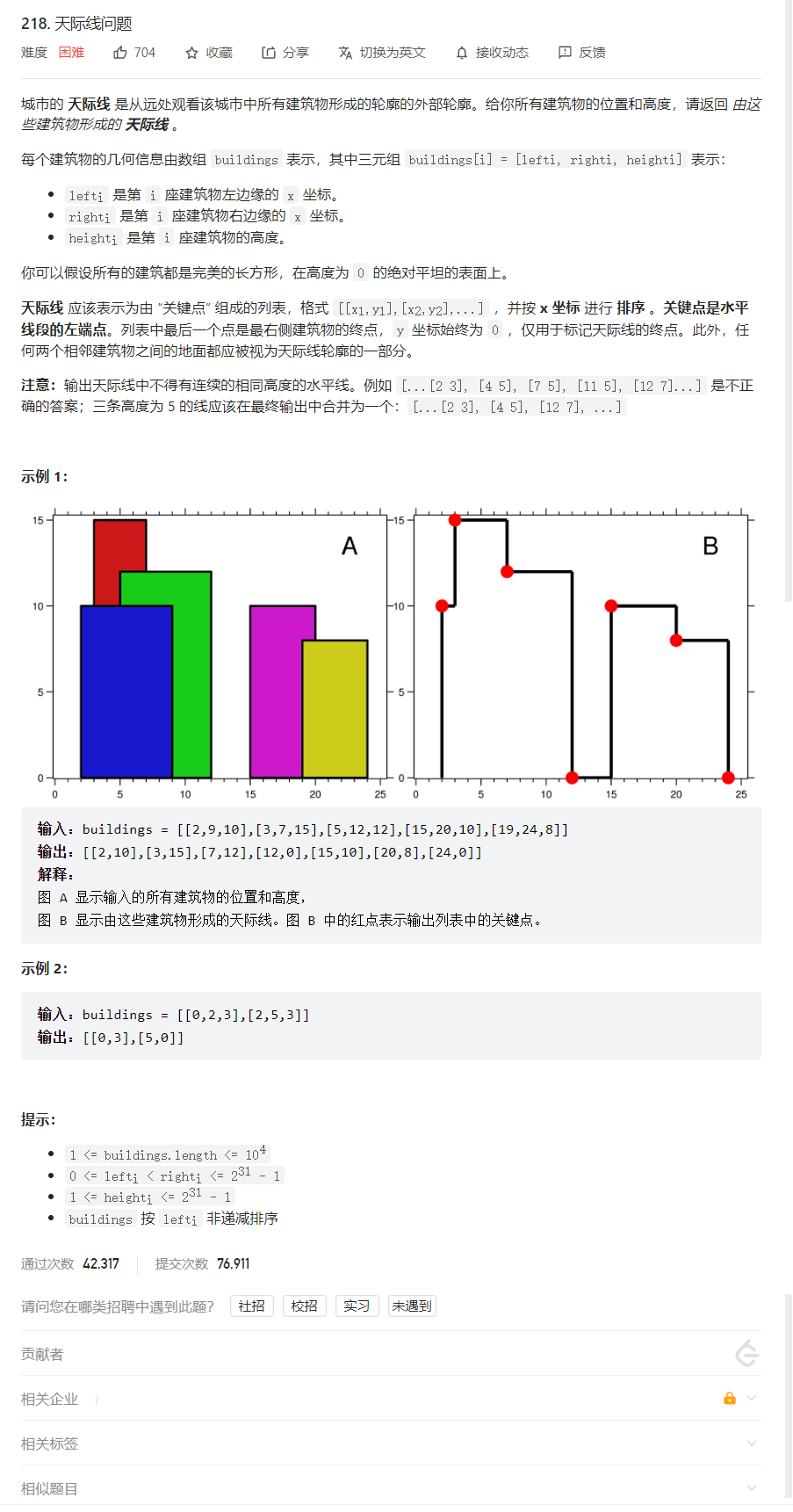
解法 1

class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        // 思路：
        // 优先队列 + 线性扫描
        // 可以看出，天际线的横坐标必为 矩形的端点 处
        // 遍历所有端点，在每个端点处，如果是左端点，将当前高度压入，参与竞争，取该端点处高度集合的最大高度
        // 若是右端点，先删除当前高度，然后取高度集合的最大高度
        List<List<Integer>> res = new ArrayList<>();
        // 保存所有端点，及各自的高度，为了后续方便判断是左端点，还是右端点，通过 '-' 符号位标识
        int len = buildings.length;
        List<int[]> array = new ArrayList<>(); // 保存 左端点 + 右端点
        // O(n)
        for(int i = 0; i < len; i ++) {
            int[] cur = buildings[i];
            int left = cur[0];
            int right = cur[1];
            int height = cur[2];
            array.add(new int[]{left, - height}); // 负号 标识
            array.add(new int[]{right, height});
        }
        // array 排序 - 升序 O(nlogn)
        Collections.sort(array, (a, b) -> {
            if(a[0] == b[0]) {
                // 若分别为 正 - 负，无影响
                // 若全为 正，先出队 小的正数，每次取 peek() 优先取到大的值
                // 若全为 负，先入队 绝对值大的数，每次 peek() 优先取到 大的值
                return a[1] - b[1]; // 端点相同时，不论正负，均按升序排列
            } else {
                return a[0] - b[0];
            }
        });
        // 遍历所有端点
        int prevHeight = -1; // 上一节点高度，去重
        PriorityQueue<Integer> queue = new PriorityQueue<>((a, b) -> {
            return b - a; // 创建大根堆
        }); // 存放的是高度
        // O(n^2)
        for(int[] cur: array) {
            int index = cur[0]; // 端点横坐标
            int height = cur[1];
            if(height < 0) {
                // 左端点 - 入队参与最大高度竞争
                queue.offer(- height);
            } else {
                // 右端点 - 取出对应的高度，不参与竞争
                queue.remove(height); // O(n) - 每次最多删除一个节点
            }
            int maxHeight = 0;
            if(!queue.isEmpty()) {
                maxHeight = queue.peek();
            }
            if(maxHeight != prevHeight) {
                // 说明是新的天际线
                List<Integer> list = new ArrayList<>();
                list.add(index);
                list.add(maxHeight);
                res.add(list);
                prevHeight = maxHeight;
            }
        }
        return res;
    }
}

---

输出 1

---

解法 2 - 优化

class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        // 思路：
        // 优先队列 + 线性扫描 + 延时删
        // 遍历 array 求最大高度的复杂度为 O(n^2)，要降低复杂度，可以从降低 remove() 操作的复杂度入手
        // 可以将要删除高度，存入 map 中，在下一步 peek() 时，判断是否是要删除的高度，如果是，在这里删除
        List<List<Integer>> res = new ArrayList<>();
        // 保存所有端点，及各自的高度，为了后续方便判断是左端点，还是右端点，通过 '-' 符号位标识
        int len = buildings.length;
        List<int[]> array = new ArrayList<>(); // 保存 左端点 + 右端点
        // O(n)
        for(int i = 0; i < len; i ++) {
            int[] cur = buildings[i];
            int left = cur[0];
            int right = cur[1];
            int height = cur[2];
            array.add(new int[]{left, - height}); // 负号 标识
            array.add(new int[]{right, height});
        }
        // array 排序 - 升序 O(nlogn)
        Collections.sort(array, (a, b) -> {
            if(a[0] == b[0]) {
                // 若分别为 正 - 负，无影响
                // 若全为 正，先出队 小的正数，每次取 peek() 优先取到大的值
                // 若全为 负，先入队 绝对值大的数，每次 peek() 优先取到 大的值
                return a[1] - b[1]; // 端点相同时，不论正负，均按升序排列
            } else {
                return a[0] - b[0];
            }
        });
        // 遍历所有端点
        int prevHeight = -1; // 上一节点高度，去重
        PriorityQueue<Integer> queue = new PriorityQueue<>((a, b) -> {
            return b - a; // 创建大根堆
        }); // 存放的是高度
        HashMap<Integer, Integer> map = new HashMap<>(); // 删除高度 - 删除次数
        // O(n^2)
        for(int[] cur: array) {
            int index = cur[0]; // 端点横坐标
            int height = cur[1];
            if(height < 0) {
                // 左端点 - 入队参与最大高度竞争
                queue.offer(- height);
            } else {
                // 右端点 - 借助 map 延时删
                if(!map.containsKey(height)) {
                    map.put(height, 1);
                    // System.out.println("delete " + height + " 1 次");
                } else {
                    int fre = map.get(height);
                    fre ++;
                    map.put(height, fre);
                    // System.out.println("delete " + height + " " + fre + " 次");
                }
            }
            int maxHeight = 0;

            while(!queue.isEmpty()) {
                // 当前高度是要删除的
                maxHeight = queue.peek();
                if(map.containsKey(maxHeight)) {
                    queue.poll();
                    int fre = map.get(maxHeight);
                    fre --;
                    if(fre == 0) {
                        map.remove(maxHeight);
                        // System.out.println("remove " + maxHeight);
                    } else {
                        map.put(maxHeight, fre);
                        // System.out.println("还需要 remove " + maxHeight + "  " + fre + " 次");
                    }
                } else {
                    break;
                }
            }
            if(queue.isEmpty()) {
                maxHeight = 0;
            }
            if(maxHeight != prevHeight) {
                // 说明是新的天际线
                List<Integer> list = new ArrayList<>();
                list.add(index);
                list.add(maxHeight);
                res.add(list);
                prevHeight = maxHeight;
            }
        }
        return res;
    }
}

---

输出 2