🌕🌕🌗 307. 区域和检索 - 数组可修改

难度: 🌕🌕🌗

问题描述

---

解法 1 - 树状数组

class NumArray {
    // 思路：
    // 树状数组 - 修改某个下标处的值时，只修改部分下标处的值；查询某个区间和时，查询部分区间- O(logN)
    // 利用公式 x & (-x) 获取需要的某些个下标，该公式可以得到 x 的最低位 1 所在的位对应的 2 的幂
    // 例：
    // x == 5 == 0 0101 ; -x = x 的补码 + 1 = 1 1010 + 1 = 1 1011 ; x & (-x) = 0 0101 & 1 1011 = 1 = 2 ^ 0
    // 由于 0 的特殊性，0 & (-0) = 0 防止造成死循环，需要从 下标 1 开始，设为 arr[len + 1]
    // 1 : 0 0001 --> 2^0 = 1
    // 2 : 0 0010 --> 2^1 = 2
    // 3 : 0 0011 --> 2^0 = 1
    // 4 : 0 0100 --> 2^2 = 4
    // 5 : 0 0101 --> 2^0 = 1
    // 6 : 0 0110 --> 2^1 = 2
    // 7 : 0 0111 --> 2^0 = 1
    // 8 : 0 1000 --> 2^3 = 8
    // 9 : 0 1001 --> 2^0 = 1
    // 10: 0 1010 --> 2^1 = 2
    // 11: 0 1011 --> 2^0 = 1
    // 12: 0 1100 --> 2^2 = 4
    // 13: 0 1101 --> 2^0 = 1
    // 14: 0 1110 --> 2^1 = 2
    // 15: 0 1111 --> 2^0 = 1
    // 可就是说，修改 | 插入 某个下标时，需要修改一条链路，假设 max(index) = 16，即 len == 17，则
    // 1 --> 2 --> 4 --> 8 --> 16
    // 3 --> 4 --> 8 --> 16
    // 5 --> 6 --> 8 --> 16
    // 7 --> 8 --> 16
    // 9 --> 10 --> 12 --> 16
    // 11 --> 12 --> 16
    // 13 --> 14 --> 16
    // 15 --> 16
    // 将这些依赖关系画成树结构，可以看出，是一颗非对称的多叉树，修改某个叶子节点，则该条树转上的值均需改变
    // 要求某个区间 [0, ?] 的区间和，那么就反向计算，用 ? - 当前的 x & (0x) 作为下一个节点，
    // 例，[0, 11] = arr[12] + arr[12 - 4] = arr[12] + arr[8]

    int[] arr;
    int[] nums;
    int len;
    public NumArray(int[] nums) {
        this.len = nums.length;
        this.nums = nums;
        arr = new int[len + 1]; // 下标 0 废弃防止出现死循环
        // 初始化 arr
        for(int i = 0; i < len; i ++) {
            insert(i + 1, nums[i]);
        }
        // System.out.println(Arrays.toString(arr));
    }

    private void insert(int index, int val) {
        // 初始化时，将初始数组的值依次插入到 arr 对应位置，此外相关链路处的值也需改变
        while(index <= len) {
            arr[index] += val;
            index = getNextIndex(index); 
        }
    }
    private int getNextIndex(int index) {
        int step = index & (-index);
        return index + step;
    }
    
    public void update(int index, int val) {
        // 更新当前下标对应一整条链路的相关值
        int diff = val - nums[index]; // 获取差值
        nums[index] = val; // 更新 nums
        insert(index + 1, diff);
    }
    
    public int sumRange(int left, int right) {
        // sum[right + 1] - sum[left]
        return getSum(right + 1) - getSum(left);
    }

    private int getSum(int end) {
        // sum[0, end - 1] = arr[end] + arr[...]
        int res = 0;
        while(end > 0) {
            res += arr[end];
            end = getPrevIndex(end);
        }
        return res;
    }
    private int getPrevIndex(int index) {
        int step = index & (-index);
        return index - step;
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(index,val);
 * int param_2 = obj.sumRange(left,right);
 */

---

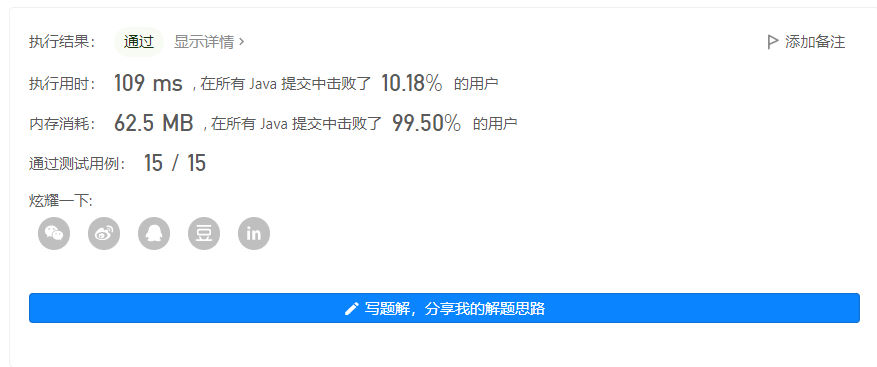
输出 1

---

解法 2 - 线段树

class NumArray {
    // 思路：
    // 线段树 - 将整个区间分成 2 部分，然后递归继续分，直到某个区间只剩一个节点
    // 修改时，修改该节点对应的整条链路
    // 如果说 树状数组是非平衡多叉树，那么 线段树 就是 平衡二叉树
    // 能用 线段树 解决的问题，树状数组不一定能够解决；但反之一定成立。
    // 因此 线段树 的功能比 树状数组 要强大

    private TreeNode root;
    int len;
    int[] nums;

    public NumArray(int[] nums) {
        len = nums.length;
        this.nums = nums;
        // 初始化线段树
        root = new TreeNode(0, len - 1, 0);
        for(int i = 0; i < len; i ++) {
            TreeNode cur = getNode(root, i);
            addDiff(cur, nums[i]);
        }
    }
    // 找到 index 对应的叶子节点
    private TreeNode getNode(TreeNode cur, int index) {
        // 递归终止条件
        if(cur.startIndex == cur.endIndex) {
            return cur;
        }
        int mid = cur.startIndex + ((cur.endIndex - cur.startIndex) >> 1);
        if(cur.left == null) {
            // 没有子节点，先进行初始化
            cur.left = new TreeNode(cur.startIndex, mid, 0);
            cur.right = new TreeNode(mid + 1, cur.endIndex, 0);
            cur.left.parent = cur;
            cur.right.parent = cur;
        }
        // 判断是往左子树找还是右子树找
        if(index <= mid) {
            return getNode(cur.left, index);
        } else {
            return getNode(cur.right, index);
        }
    }
    // 从叶子节点开始，往上修改整条链路的值
    private void addDiff(TreeNode cur, int diff) {
        cur.val += diff;
        // 已经到达根节点，修改完根节点后直接返回
        if(cur.parent == null) {
            return;
        } else {
            addDiff(cur.parent, diff);
        }
    }
    
    public void update(int index, int val) {
        int diff = val - nums[index];
        nums[index] = val;
        TreeNode cur = getNode(root, index);
        addDiff(cur, diff);
    }
    
    public int sumRange(int left, int right) {
        return getSum(root, left, right);
    }

    private int getSum(TreeNode cur, int startIndex, int endIndex) {
        // 递归终止条件
        if(cur.startIndex == startIndex && cur.endIndex == endIndex) {
            return cur.val;
        }
        // 判断是包含一个子树 还是 两个子树 均有部分
        int mid = cur.startIndex + ((cur.endIndex - cur.startIndex) >> 1);
        if(endIndex <= mid) {
            // 只有左子树
            return getSum(cur.left, startIndex, endIndex);
        } else if(startIndex > mid) {
            // 只有右子树
            return getSum(cur.right, startIndex, endIndex);
        } else {
            // 两个子树均有部分要求和
            return getSum(cur.left, startIndex, mid) + getSum(cur.right, mid + 1, endIndex);
        }
    }
}

// 构造线段树节点类
class TreeNode {
    int startIndex;
    int endIndex;
    int val; // [startIndex, endIndex] 区间和
    
    TreeNode parent; // 除了需要往下递归，在更新节点时，还需要往上递归更新父节点值
    TreeNode left;
    TreeNode right;

    public TreeNode(int startIndex, int endIndex, int val) {
        this.startIndex = startIndex;
        this.endIndex = endIndex;
        this.val = val;
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(index,val);
 * int param_2 = obj.sumRange(left,right);
 */

---

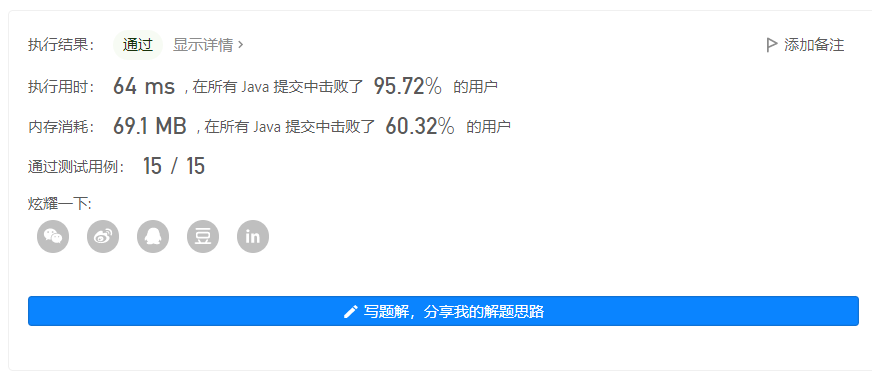
输出 2