🌕 🌕 🌕 🌕 327. 区间和的个数

难度: 🌕 🌕 🌕 🌕

问题描述

---

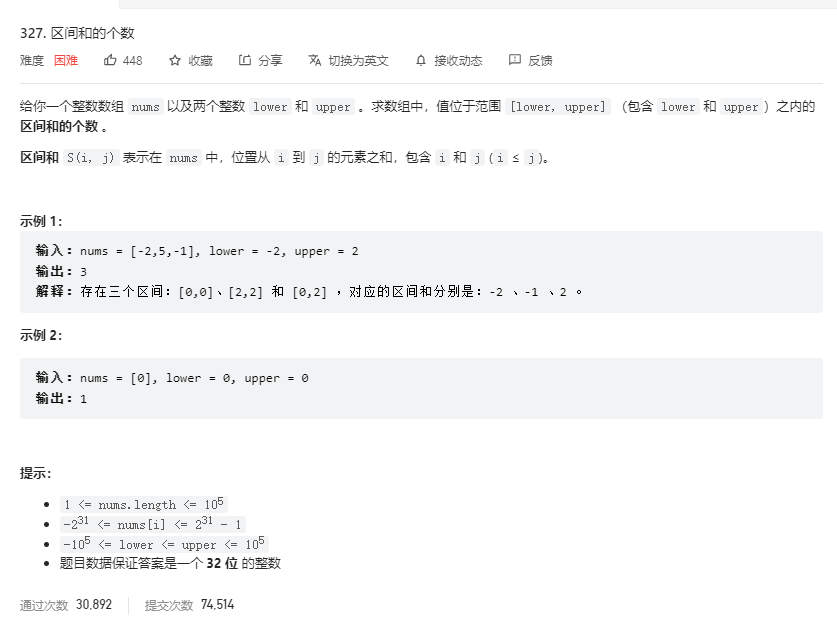
解法

class Solution {
    public int countRangeSum(int[] nums, int lower, int upper) {
        // 思路：
        // 要求 sum[left, right] ∈ [lower, upper] 
        // 首先想到的就是 前缀和 sum[left, right] = arr[right + 1] - arr[left] ∈ [lower, upper] 
        // 如果遍历数组求出 前缀和 数组，然后 2 层循环，
        // 固定 i，让 j 从 i + 1 开始一直遍历到 len - 1， 找出满足条件的区间个数
        // 如此，复杂度为 O(N^2)

        // 现在我们需要思考如何降低复杂度？
        // 如果数组全为正数，那么 前缀和数组就是 单调递增 的
        // 在一个 单增数组 中如何找到区间 [left, right + 1] 使得两个边界之差 ∈ [lower, upper] ？
        // 仍然固定 i，让 m & n 从 i + 1 开始一直遍历，找到右边界的 上界 m & 下界 n，即 {[i, m], [i, m + 1], ..., [i, n]}
        // 当 i 确定时，满足条件的区间个数为 n - m + 1
        // 向后移动 i，由于 数组单增，因此 m & n 无需再次从 i + 1 开始找，而是从 原来位置继续往后遍历即可
        // 为什么？ ∵ i ++ 后，arr[i] 增大，要使得 arr[m] - arr[i] >= lower，因此 arr[m] 也需增大，从而 m 指针只需后移
        // 因此该遍历使得 i & m & n 只需一次遍历即可找到所有满足条件的区间和
        // 即，复杂度由 无序数组的 O(N^2) --> 有序数组的 O(N) 

        // 如何保证前缀和数组 为有序数组？
        // 通过 归并排序 将数组变为有序，且总复杂度不会超过 O(N^2)

        // 对前缀和数组 排序 会影响原来数组的区间和结果吗？
        // 即，排序后的前缀和数组中求得的 区间和 & 未排序的前缀和数组中实际的 区间和 结果相同吗？
        // 答：结果相同
        // 分析：
        // 在归并排序递归的过程中，进行到当前数组，我们可以直接得出
        // 左半区间满足条件的区间和个数 + 右半区间满足条件的区间和个数
        // 在单层递归逻辑中，我们需要求 跨左半区间 & 右半区间 这一部分的满足条件的区间和的个数

        // 例：原数组 [-2, 5, -1] --> 前缀和数组 [0, -2, 3, 2]，lower = -2, upper == 2
        // 针对原始前缀和数组，我们可以得到满足条件的区间为：
        // 1) [0, -2] 对应原数组的 [-2]
        // 2) [0, 2] 对应原数组的 [-2, 5, -1]
        // 3) [3, 2] 对应原数组的 [-1]
        // 递归过程中前缀和数组经历 [0, -2], [3, 2] --> {[0], [-2]}, {[3], [2]}
        // 然后开始进行当前轮的区间和，由于 左半区间 & 右半区间 均只有一个值，因此 left = right = 0
        // 针对 {[0], [-2]}，i = 0, m = 1, n = 1，即存在一个满足条件的区间和，就是 1) [0, -2]
        // 针对 {[3], [2]}，i = 0, m = 1, n = 1，即存在一个满足条件的区间和，就是 3) [3, 2]
        // 然后进行归并，使得当前轮前缀和升序，得到 前缀和数组 [-2, 0], [2, 3]
        // 其中 f([-2, 0]) = 1 --> 存在 1 个满足条件的区间和；f([2, 3]) = 1
        // 递归到上一层，进行当前轮的区间和，此时 left = right = 1
        // 针对 {[-2, 0], [2, 3]} i = 1, m = 2, n = 2 即存在一个满足条件的区间和，就是 2) [0, 2]
        // 然后进行归并，保证当前轮前缀和单增，得到 前缀和数组 [-2, 0, 2, 3]
        // 其中 f([-2, 0, 2, 3]) = left + right + 1 = 3 无后续递归，返回结果 == 3

        // 可以看出，左半区间满足条件的区间和个数 & 右半区间满足条件的区间和个数 是递归得到的
        // 单层递归逻辑中，重点是得到 跨左半区间 & 右半区间 这一部分的满足条件的区间和的个数
        // 由于 左半区间 & 右半区间 得到时，就是已经排好序的前缀和数组
        // 问题就转换为：
        // 针对 左半区间 & 右半区间 各自排序，是否影响 跨区间得到的 满足条件的区间和个数？
        // 可以想象，我们关注的不是中间的顺序，而是保证 [i, m | n] 的边界值之差满足条件，即 diff = arr[m | n] - arr[i] ∈ [lower, upper]
        // 而 i 比在左半区间，m | n 比在 右半区间
        // 只要 [i, m] 满足条件，那么不论左半区间的 i 移动到左半区间的哪里，
        // arr[i] 的值肯定不变，因为前缀和的元素从一开始求出后，我们之后没有改变过元素的值，而是改变的顺序
        // 所以 arr[m | n] - arr[i] = diff 的值恒存在
        // 即无论是否修改 左 | 右 区间各自的元素顺序，满足条件的区间和的个数一定是恒定值，是固定不变的

        int len = nums.length;
        long[] arr = new long[len + 1]; // 虽然每个元素均在 int 范围内，但无法保证前缀和也在 int 范围内
        // 初始化 arr[]
        for(int i = 1; i <= len; i ++) {
            arr[i] = arr[i - 1] + nums[i - 1];
        }
        return mySol(arr, lower, upper, 0, len);
    }

    private int mySol(long[] arr, int lower, int upper, int left, int right) {
        // 返回的是当前区间的区间和个数，同时将前缀和数组排序
        // 递归终止条件
        if(left >= right) {
            return 0; // 只有一个值，由于是前缀和数组，需要两数做差才可得到某个区间，因此一个元素不存在区间这一概念
        }
        int mid = left + ((right - left) >> 1);
        int l = mySol(arr, lower, upper, left, mid); // 左半区间满足条件的区间和个数
        int r = mySol(arr, lower, upper, mid + 1, right);
        // 单层递归逻辑 - 求 跨区间 满足条件的区间和个数
        int i = left; // 左半区间指针，每次固定 i，移动 m & n
        int m = mid + 1; 
        int n = mid + 1;
        int res = l + r;
        while(i <= mid && m <= right) {
            // 求 m -- arr[m] - arr[i] >= lower
            while(m <= right && arr[m] - arr[i] < lower) {
                m ++;
            }
            // 求 n -- arr[n] - arr[i] <= upper
            n = Math.max(n, m); // 保证 arr[n] - arr[i] >= lower，然后求高区间
            while(n <= right && arr[n] - arr[i] <= upper) {
                n ++;
            }
            res += n - m; // [m, n) 不包含 n
            i ++;
        }
        // 排序 前缀和数组
        if(arr[mid] <= arr[mid + 1]) {
            // 已经是排好序的数组，无需排序
        } else {
            merge(arr, left, mid, right);
        }
        return res;
    }

    private void merge(long[] arr, int left, int mid, int right) {
        int len = right - left + 1;
        long[] res = new long[len]; // 暂存排序好的数组
        int index = 0;
        int i = left;
        int j = mid + 1;
        while(i <= mid && j <= right) {
            if(arr[i] <= arr[j]) {
                res[index] = arr[i];
                i ++;
                index ++;
            } else {
                res[index] = arr[j];
                j ++;
                index ++;
            }
        }
        while(i <= mid) {
            res[index] = arr[i];
            i ++;
            index ++;
        }
        while(j <= right) {
            res[index] = arr[j];
            j ++;
            index ++;
        }
        for(int k = 0; k < len; k ++) {
            arr[k + left] = res[k];
        }
    }
}

---

输出