🌕🌗 493. 翻转对

难度: 🌕🌗

问题描述

---

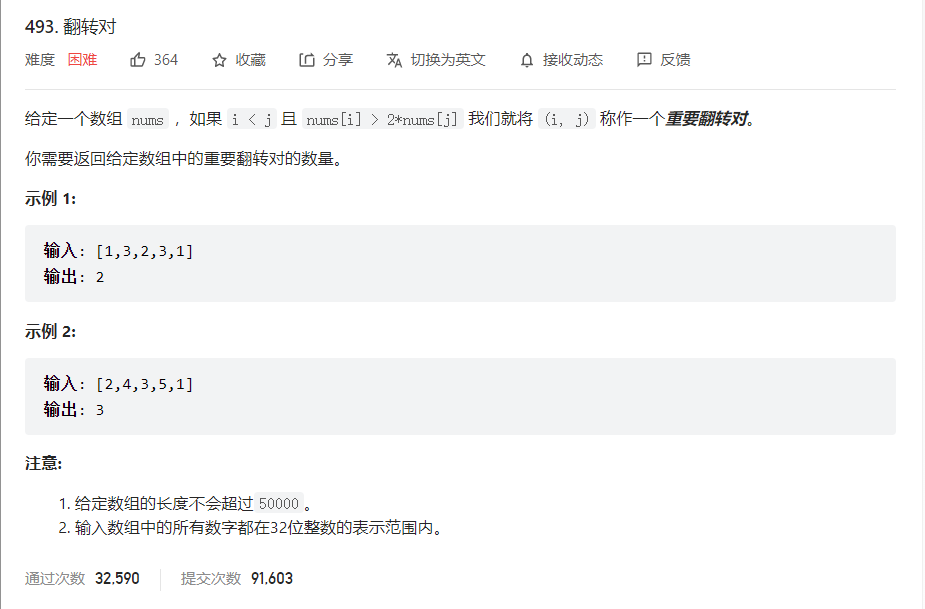
解法

class Solution {
    public int reversePairs(int[] nums) {
        // 思路：
        // 归并排序
        // 在递归的过程中由于左右半区间均已排好序，因此在单层逻辑中通过一次遍历获得当前层的翻转对个数
        // 在判断 2[j] 时防止超范，例 [2147483647,2147483647,2147483647,2147483647,2147483647,2147483647]
        int len = nums.length;
        return mySol(nums, 0, len - 1);
    }

    private int mySol(int[] nums, int left, int right) {
        // 递归终止条件
        if(left >= right) {
            return 0; // 只有一个元素，不存在翻转对
        }
        int mid = left + ((right - left) >> 1);
        int l = mySol(nums, left, mid);
        int r = mySol(nums, mid + 1, right);
        int res = l + r;
        // [i] > 2[j] --> 固定 j，从左到右找 [m, n] 满足 {[m, j], [m + 1, j], ..., [n, j]} 
        // 正是由于 左右区间 各自有序，才可做到 一遍遍历，从而降低复杂度
        int j = mid + 1;
        int m = left;
        int n = left;
        while(j <= right && m <= mid) {
            // 找 m --> [m] > 2[j]
            while(m <= mid && (long)nums[m] <= 2l * nums[j]) {
                m ++;
            }
            // 找 n --> [n] > 2[j]
            n = Math.max(m, n);
            while(n <= mid && (long)nums[n] > 2l * nums[j]) {
                n ++;
            }
            // [m, n)
            res += n - m;
            j ++;
        }
        if(nums[mid] <= nums[mid + 1]) {
            //
        } else {
            merge(nums, left, mid, right);
        }
        return res;
    }

    private void merge(int[] nums, int left, int mid, int right) {
        int len = right - left + 1;
        int[] res = new int[len];
        int index = 0;

        int i = left;
        int j = mid + 1;
        while(i <= mid && j <= right) {
            if(nums[i] <= nums[j]) {
                res[index] = nums[i];
                i ++;
                index ++;
            } else {
                res[index] = nums[j];
                j ++;
                index ++;
            }
        }
        while(i <= mid) {
            res[index] = nums[i];
            i ++;
            index ++;
        }
        while(j <= right) {
            res[index] = nums[j];
            j ++;
            index ++;
        }
        for(int k = 0; k < len; k ++) {
            nums[k + left] = res[k];
        }
    }
}

---

输出