🌕🌕🌗 164. 最大间距

难度: 🌕🌕🌗

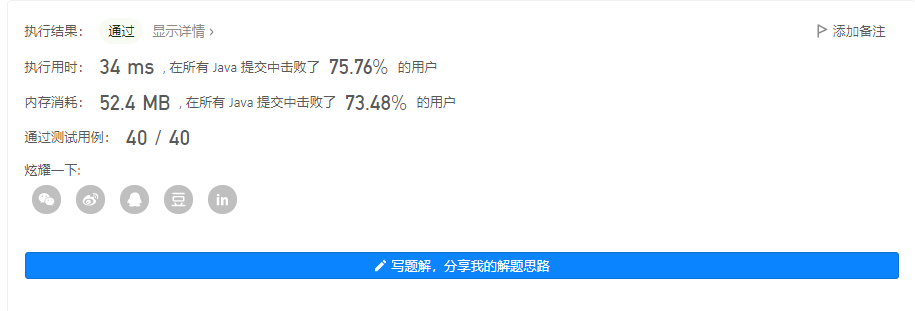
问题描述

---

解法

class Solution {
    public int maximumGap(int[] nums) {
        // 思路：
        // 桶排序 
        // 桶的个数非数组长度，这样容易出现特大的数在一个小的下标前面，需要维护各个下标的链表，和前后链表的数比较才可判断
        // 桶的个数由间距确定，可以看出，若是所有数均等间距排列，则 step == (max - min) / (len - 1) 
        // 只要有一个不等间距排列，那么必有一个最小值，和对应的最大值，因此 max step > (max - min) / (len - 1)
        // 桶个数 == (max - min) / (step + 1) ，尽可能保证数据在不同桶中，max step 必占据至少 2 个桶，
        // 即，max step 只能在相邻非空桶中，要么是当前桶和前面的某个非空桶，要么是和后面的某个非空桶
        int len = nums.length;
        if(len < 2) {
            return 0;
        }
        if(len == 2) {
            return Math.abs(nums[0] - nums[1]);
        }
        // len > 2
        int max = nums[0];
        int min = nums[0];
        for(int i : nums) {
            max = Math.max(max, i);
            min = Math.min(min, i);
        }
        if(max == min) {
            return 0; // max == min 所有元素值相等
        }

        int step = (max - min) / (len - 1);
        if(step == 0) {
            step = 1; // 前面已经证明过 max != min，若 step 仍 == 0 说明分子过小，分母过大但仍 < len
        }
        int size = (max - min) / step + 1;

        // 创建桶
        int[][] bucket = new int[size][2]; // 只需要保留下标下 min & max，肯定不会出现特大值分配在该桶中的情况
        for(int i = 0; i < size; i ++) {
            Arrays.fill(bucket[i], -1);
        }
        for(int i : nums) {
            int index = (i - min) / step;
            if(bucket[index][0] == -1) {
                // 说明还没有元素在里面
                bucket[index][0] = i;
                bucket[index][1] = i;
            } else {
                bucket[index][0] = Math.min(bucket[index][0], i);
                bucket[index][1] = Math.max(bucket[index][1], i);
            }
        }
        // 遍历桶
        // System.out.println(Arrays.toString(bucket[0]));
        // System.out.println(Arrays.toString(bucket[33]));
        int res = -1;
        for(int i = 0; i < size;) {
            int[] cur = bucket[i];
            // 每次和后面的非空桶比较
            int next = i + 1;
            while(next < size && bucket[next][0] == -1) {
                next ++;
            }
            if(next == size) {
                return res;
            }
            // 当前桶的最大值 & 下一个桶的最小值 比较
            int diff = bucket[next][0] - cur[1];
            res = Math.max(res, diff);
            i = next;
        }
        return res;
    }
}

---

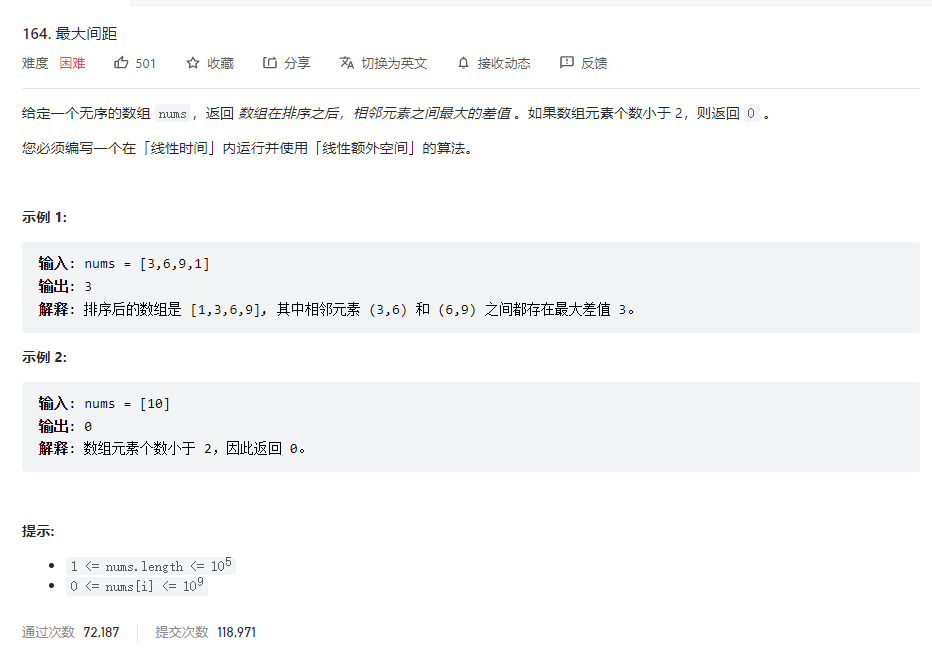
输出