🌕 1365. 有多少小于当前数字的数字

难度: 🌕

问题描述

---

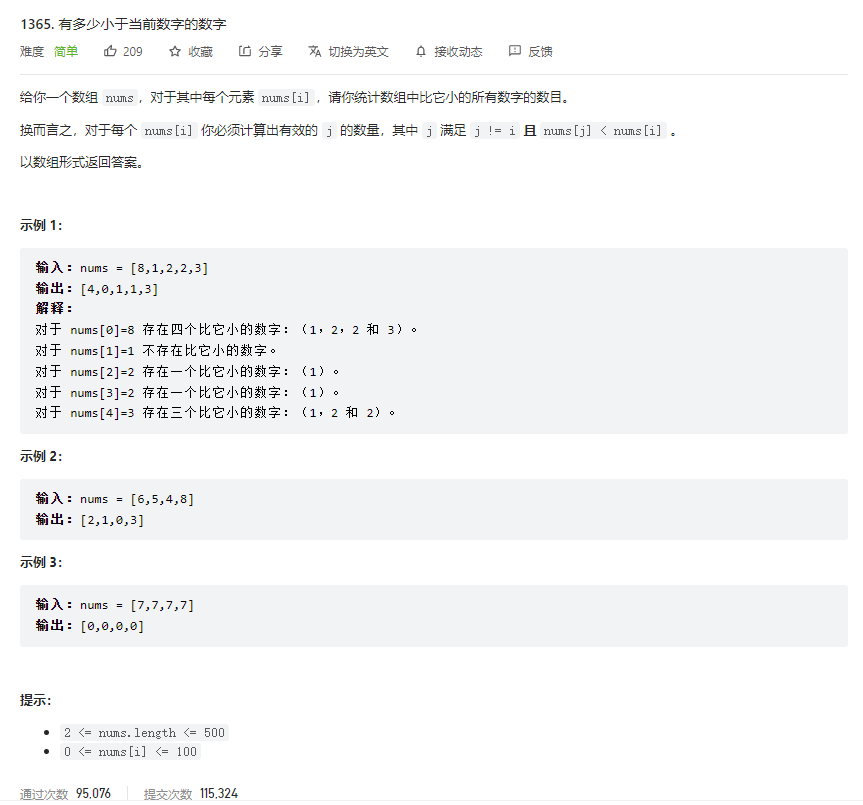
解法 1 - 快排

class Solution {
    public int[] smallerNumbersThanCurrent(int[] nums) {
        // 思路：
        // 暴力搜索 - 2 层遍历 - O(N^2)
        // 降低复杂度 - 数组排序 - 存 map
        // method 1 - 快排
        int len = nums.length;
        int[] array = new int[len];
        System.arraycopy(nums, 0, array, 0, len);
        mySol(array, 0, len - 1);
        // System.out.println(Arrays.toString(array));
        // 遍历存 map
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < len; i ++) {
            int cur = array[i];
            if(!map.containsKey(cur)) {
                map.put(cur, i);
            } 
        }
        int[] res = new int[len];
        for(int i = 0; i < len; i ++) {
            res[i] = map.get(nums[i]);
        }
        return res;
    }

    private void mySol(int[] nums, int left, int right) {
        // 递归终止条件
        if(left >= right) {
            return;
        }
        // left < right
        // 找基准，左边的都比它小，右边的都比它大
        int monitor = nums[left];
        int i = left;
        int j = right;
        while(i < j) {
            // 从右到左找比基准小的数，这里必须包含等号
            while(i < j && nums[j] >= monitor) {
                j --;
            }
            while(i < j && nums[i] <= monitor) {
                i ++;
            }
            swap(nums, i, j);
        }
        // left == right
        swap(nums, left, i);
        // 递归，快排两边
        mySol(nums, left, i - 1);
        mySol(nums, i + 1, right);
    }

    private void swap(int[] nums, int left, int right) {
        int tmp = nums[left];
        nums[left] = nums[right];
        nums[right] = tmp;
    }
}

---

输出 1

#

解法 2 - 归并排序

class Solution {
    public int[] smallerNumbersThanCurrent(int[] nums) {
        // 思路：
        // 暴力搜索 - 2 层遍历 - O(N^2)
        // 降低复杂度 - 数组排序 - 存 map
        // method 2 - 归并排序
        int len = nums.length;
        int[] array = new int[len];
        System.arraycopy(nums, 0, array, 0, len);
        mySol(array, 0, len - 1);
        // System.out.println(Arrays.toString(array));
        // 遍历存 map
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < len; i ++) {
            int cur = array[i];
            if(!map.containsKey(cur)) {
                map.put(cur, i);
            } 
        }
        int[] res = new int[len];
        for(int i = 0; i < len; i ++) {
            res[i] = map.get(nums[i]);
        }
        return res;
    }

    private void mySol(int[] nums, int left, int right) {
        // 递归终止条件
        if(left >= right) {
            return;
        }
        // left < right
        // 分治
        int mid = left + ((right - left) >> 1);
        mySol(nums, left, mid);
        mySol(nums, mid + 1, right);
        // 合并
        merge(nums, left, mid, right);
    }

    private void merge(int[] nums, int left, int mid, int right) {
        // left - 左数组左边界
        // mid - 左数组右边界
        // right - 右数组右边界
        int len = right - left + 1;
        int[] res = new int[len]; // 暂存排序好的数组
        int i = left;
        int j = mid + 1;
        int index = 0;
        while(i <= mid && j <= right) {
            if(nums[i] <= nums[j]) {
                res[index] = nums[i];
                index ++;
                i ++;
            } else {
                res[index] = nums[j];
                index ++;
                j ++;
            }
        }
        while(i <= mid) {
            res[index] = nums[i];
            index ++;
            i ++;
        }
        while(j <= right) {
            res[index] = nums[j];
            index ++;
            j ++;
        }
        // 将排序好的 res 赋值回 nums 对应位置
        System.arraycopy(res, 0, nums, left, len);
    }

    private void swap(int[] nums, int left, int right) {
        int tmp = nums[left];
        nums[left] = nums[right];
        nums[right] = tmp;
    }
}

---

输出 2

---

解法 3 - 堆排

class Solution {
    public int[] smallerNumbersThanCurrent(int[] nums) {
        // 思路：
        // 暴力搜索 - 2 层遍历 - O(N^2)
        // 降低复杂度 - 数组排序 - 存 map
        // method 3 - 堆排
        int len = nums.length;
        int[] array = new int[len];
        System.arraycopy(nums, 0, array, 0, len);
        // 初始化大根堆
        init(array, len);
        // 将大根堆平铺成有序数组的形式
        for(int i = len - 1; i > 0; i --) {
            // 起始下标始终为最大值，将它和末尾没排好序的下标交换，重新调整，维护大根堆
            swap(array, 0, i);
            // 维护 [0, i - 1] 区间大根堆
            mySol(array, 0, i - 1);
        }
        // System.out.println(Arrays.toString(array));
        // 遍历存 map
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < len; i ++) {
            int cur = array[i];
            if(!map.containsKey(cur)) {
                map.put(cur, i);
            } 
        }
        int[] res = new int[len];
        for(int i = 0; i < len; i ++) {
            res[i] = map.get(nums[i]);
        }
        return res;
    }

    private void init(int[] nums, int len) {
        // 初始化 - 构造大根堆
        // 遍历数组，依次加入已经维护好的大根堆
        // 首节点本身就是一个堆，下标从 1 开始
        // n 节点的 left = 2n + 1， right = 2n + 2
        // m 节点的父节点 = (n - 1) / 2
        for(int i = 1; i < len; i ++) {
            int cur = i;
            int fIndex = (cur - 1)>> 1; // 父节点下标
            if(nums[cur] <= nums[fIndex]) {
                continue; // 无需调整
            }
            while(i > 0 && fIndex >= 0 && nums[cur] > nums[fIndex]) {
                swap(nums, cur, fIndex);
                cur = fIndex;
                fIndex = (cur - 1) >> 1;
            } 
        }
    }

    private void mySol(int[] nums, int left, int right) {
        // 判断当前元素是否要下沉
        int cur = left;
        int leftChild = 2 * cur + 1;
        int rightChild = 2 * cur + 2;
        // 判断孩子是否超范
        if(leftChild > right) {
            return;
        }
        // 至少还存在一个孩子在边界中
        int maxChildIndex = leftChild;
        // 取左右孩子值最大的孩子对应的下标
        if(rightChild <= right && nums[rightChild] > nums[leftChild]) {
            maxChildIndex = rightChild;
        }
        // 跟最大孩子的值比较，判断是否下沉
        if(nums[cur] >= nums[maxChildIndex]) {
            return;
        }
        // 需要进行下沉操作
        swap(nums, cur, maxChildIndex);
        // 修改当前 cur
        cur = maxChildIndex;
        mySol(nums, cur, right); // 递归
    }

    private void swap(int[] nums, int left, int right) {
        int tmp = nums[left];
        nums[left] = nums[right];
        nums[right] = tmp;
    }
}

---

输出 3