🌕🌕 220. 存在重复元素 III

难度: 🌕🌕

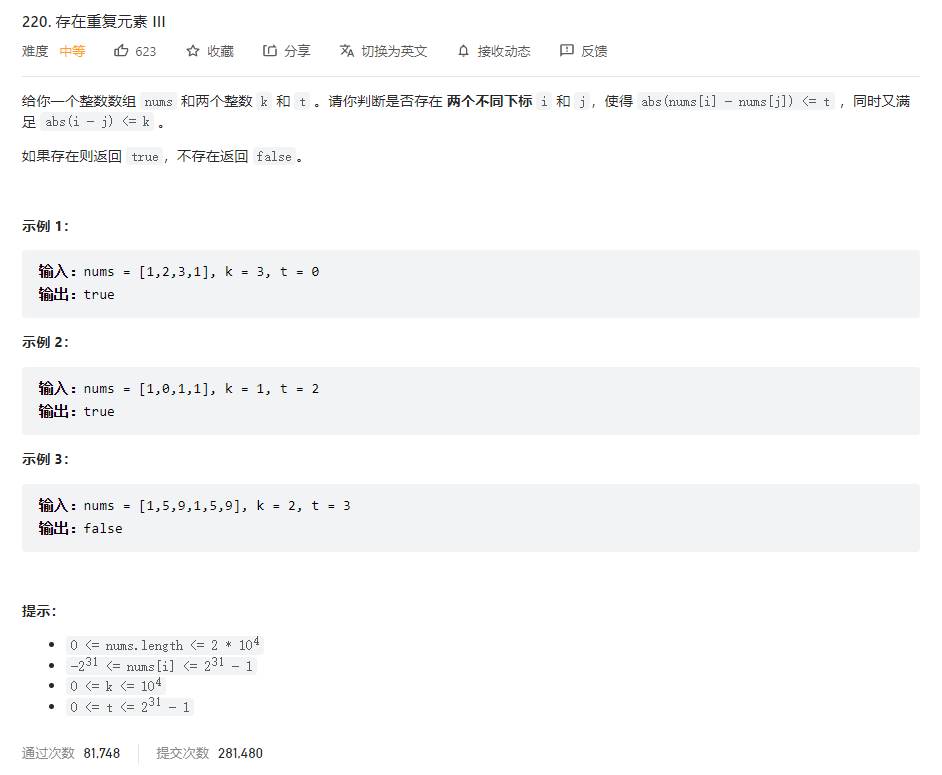
问题描述

---

解法 1 - 滑动窗口 + TreeSet

class Solution {
    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        // 思路：
        // 滑动窗口 - 保证 abs(i - j) <= k
        // 在滑动窗口内维护有序集合 - 借助 TreeSet
        // 当遍历到当前点时，找到有序集合中是否存在 [x - t, x + t] 范围内的值
        int len = nums.length;
        TreeSet<Long> set = new TreeSet<>();
        for(int i = 0; i < len; i ++) {
            long cur = (long)nums[i];
            Long floor = set.floor(cur); // 返回比 cur 小，但最接近于 cur 的值
            if(floor != null && cur - floor <= t) {
                return true;
            } 
            Long ceil = set.ceiling(cur); // 返回比 cur 大，但最接近于 cur 的值
            if(ceil != null && ceil - cur <= t) {
                return true;
            }
            set.add(cur);
            if(i >= k) {
                // 说明已经是窗口了，需要删除前面的值
                set.remove((long)nums[i - k]);
            }
        }
        return false;
    }
}

---

输出 1

---

解法 2 - 桶排序

class Solution {
    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        // 思路：
        // 桶排序
        // 当遍历到某个点时，需要判断是否有值存在于区间 [x - t, x + t]
        // 那么可以通过将 [x, x + t] 范围内的所有值映射到一个桶里，
        // 若是桶中已经有元素，说明满足条件
        // 若是相邻桶中有元素，且 x - prev || next - x 满足区间条件，说明也满足要求
        // 如何将 [x, x + t] 映射到一个桶中，即桶中存放元素的步长为多少？
        // 可以假设，x == 0，
        // 则 [0, t] 在 buchet[0] 处，[t + 1, 2t] 在 bucket[1] 处
        // [-t - 1, -1] 在 bucket[-1] 处 
        // 因此，step = t + 1
        int len = nums.length;
        // 为防止桶数组过长，因此采用 HashMap 实现桶 下标 - 值
        HashMap<Long, Long> map = new HashMap<>(); // 防止 两个 int 相减超范
        long step = t + 1;
        for(int i = 0; i < len; i ++) {
            long cur = (long)nums[i];
            long index = getIndex(cur, step);
            // System.out.println(cur + "  " + index);
            if(map.containsKey(index)) {
                return true;
            } 
            // 查找相邻桶
            if(map.containsKey(index - 1)) {
                long prev = map.get(index - 1);
                if(cur - prev <= t) {
                    return true;
                }
            }
            if(map.containsKey(index + 1)) {
                long next = map.get(index + 1);
                if(next - cur <= t) {
                    return true;
                }
            }
            // 将当前值，放入对应桶中
            map.put(index, cur);
            if(i >= k) {
                // 删除旧边界元素
                map.remove(getIndex((long)nums[i - k], step));
            }
        }
        return false;
    }

    private long getIndex(Long cur, long step) {
        if(cur >= 0) {
            return cur/step;
        } else {
            return (cur + 1)/step - 1; // 区间右移一位，然后减一
        }
    }
}

---

输出 2