🌕🌕 229. 多数元素 II

难度: 🌕🌕

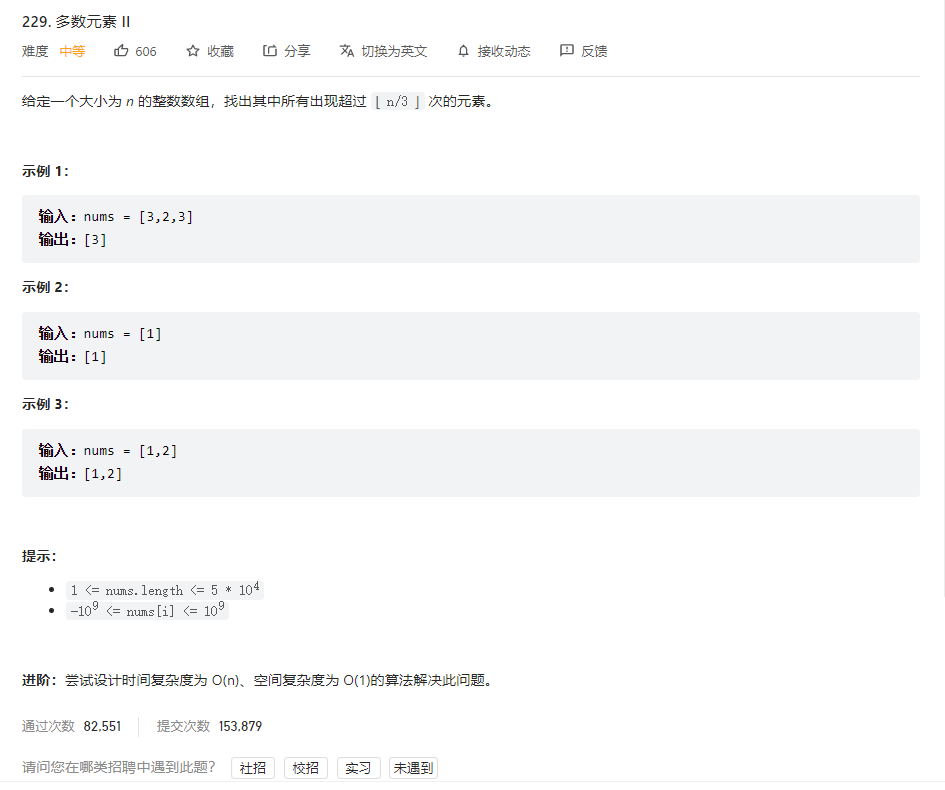
问题描述

---

解法

class Solution {
    public List<Integer> majorityElement(int[] nums) {
        // 思路：
        // 摩尔投票法
        // 分为 候选人A & 候选人B & 其他候选人
        // 当投给 A | B 时，对应票数增加
        // 当投给 其他候选人时， A & B 对应票数均减少
        // 由于 A > n/ 3 && B > n/3 所以抵消其他候选人的票数后，票数仍 > 0
        // 最多出现 2 名候选人，最少一名候选人
        int len = nums.length;
        List<Integer> res = new ArrayList<>();

        int a = 0;
        int ac = 0; // 由于初始票数为 0，所以候选人是哪位均无影响
        int b = 0;
        int bc = 0;

        for(int i = 0; i < len; i ++) {
            int cur = nums[i];
            if(cur == a) {
                ac ++;
                continue; // 直接跳出当前循环，不用考虑是否 == b，这样可以区分 a & b
            }
            if(cur == b) {
                bc ++;
                continue;
            }
            // 投的是其他候选人
            if(ac == 0) {
                // 需要更换候选人
                a = nums[i];
                ac = 1;
                continue;
            }
            if(bc == 0) {
                b = nums[i];
                bc = 1;
                continue;
            }
            // ac > 0 && bc > 0
            ac --;
            bc --;
        }

        // 再次遍历，验证 a & b 是否满足 > n/3 的条件，因此以上只是找出如果存在，那么只能在 a, b 之间
        ac = 0;
        bc = 0;
        for(int i = 0; i < len; i ++) {
            if(nums[i] == a) {
                ac ++;
            }
            if(a != b && nums[i] == b) {
                bc ++;
            }
        }

        if(3 * ac > len) {
            res.add(a);
        }
        if(3 * bc > len) {
            res.add(b);
        }
        return res;
    }
}

---

输出