🌕🌗 436. 寻找右区间

难度: 🌕🌗

问题描述

---

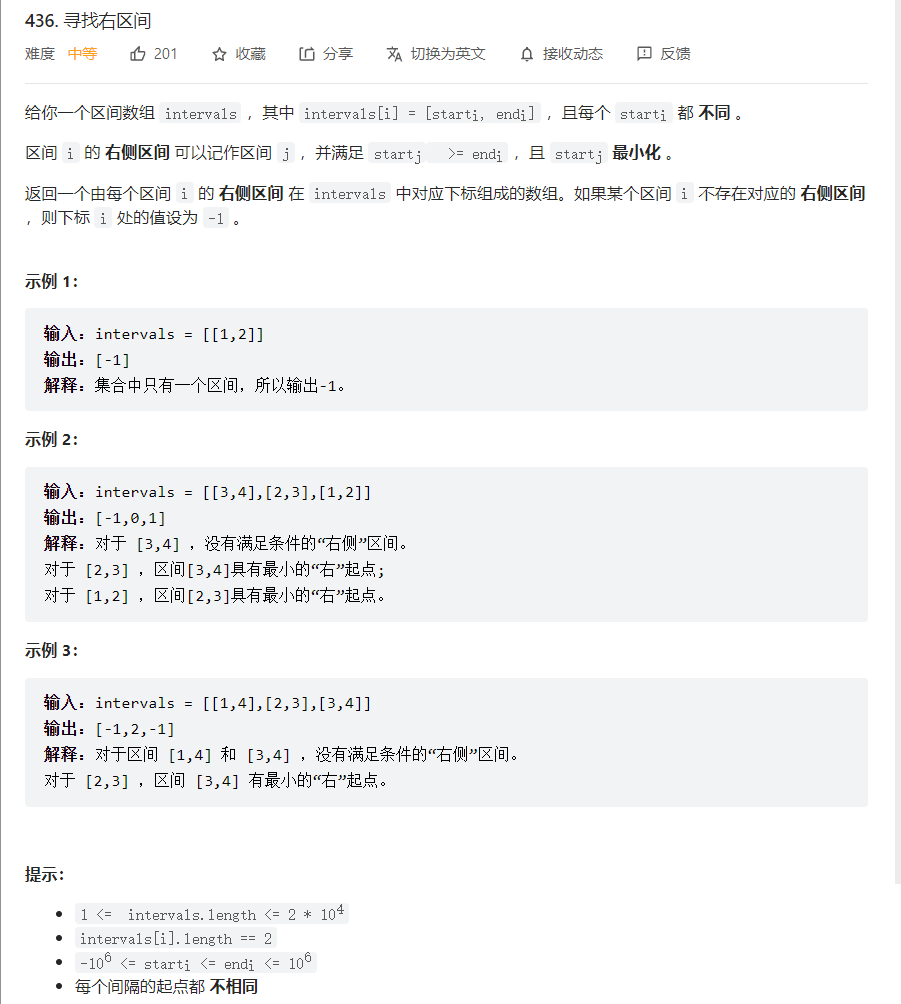
解法

class Solution {
    public int[] findRightInterval(int[][] intervals) {
        // 思路：
        // 排序 + 二分
        // 题意理解：
        // 假设当前区间为 cur[0, 1]，那么想要找的右侧区间 next[0, 1] 满足条件：
        // next[0] >= cur[1]
        // 想要找的最准确的右侧区间为集合中 左边界值 最小的区间
        // 如何求解？
        // 遍历数组，当前区间为 {cur[0], cur[1]}，我们希望找到右侧区间
        // 那么就是在所有区间中，找到 最接近 cur[1] && [0] > cur[1] 的值所对应的区间的数组下标
        int len = intervals.length;
        int[][] arr = new int[len][2];
        // 构造 [start, index] 数组并排序
        for(int i = 0; i < len; i ++) {
            int[] cur = intervals[i];
            arr[i] = new int[] {cur[0], i};
        }
        Arrays.sort(arr, (a, b) -> {
            return a[0] - b[0]; // 左边界无重复，升序
        });
        // 遍历
        int[] res = new int[len];
        for(int i = 0; i < len; i ++) {
            int[] cur = intervals[i];
            int target = cur[1];
            // 找到 最接近 target && >= target 的区间
            if(target > arr[len - 1][0]) {
                res[i] = -1;
            } else {
                res[i] = mySol(arr, target, 0, len - 1);
            }
        }
        return res;
    }

    private int mySol(int[][] arr, int target, int left, int right) {
        // 递归终止条件
        if(left >= right) {
            return arr[left][1];
        }
        // left < right
        int mid = left + ((right - left) >> 1);
        if(target == arr[mid][0]) {
            return arr[mid][1];
        } else if(target < arr[mid][0]) {
            return mySol(arr, target, left, mid);
        } else {
            return mySol(arr, target, mid + 1, right);
        }
    }
}

---

输出