🌕🌗 287. 寻找重复数

难度: 🌕🌗

问题描述

---

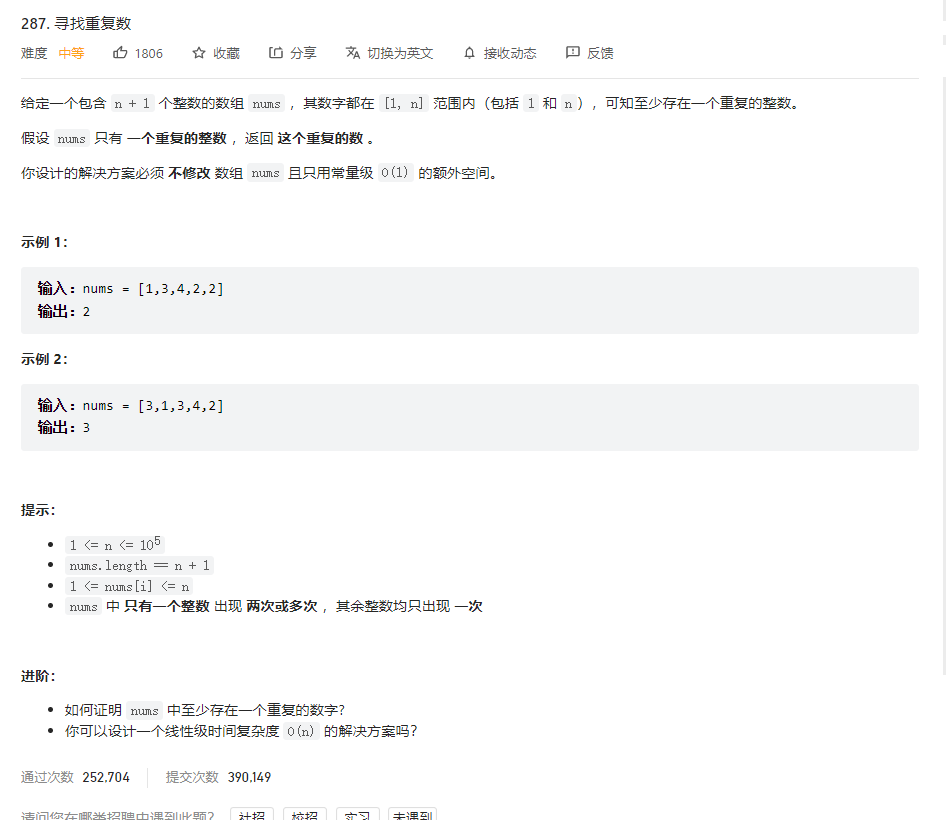
解法 1 - 不符合题意

class Solution {
    public int findDuplicate(int[] nums) {
        // 思路：
        // 原地交换
        int len = nums.length; // [0, len - 1] 正好每个下标存放一个数，有个下标存在 2 个数
        int index = 0;
        while(index < len) {
            if(nums[index] == index) {
                index ++;
            } else {
                if(nums[index] == nums[nums[index]]) {
                    // 说明要交换的2个值相等
                    return nums[index];
                } else {
                    swap(nums, index, nums[index]);
                }
            }
        }
        return len;
    }

    private void swap(int[] nums, int a, int b) {
        int tmp = nums[a];
        nums[a] = nums[b];
        nums[b] = tmp;
    }
}

---

输出 1

---

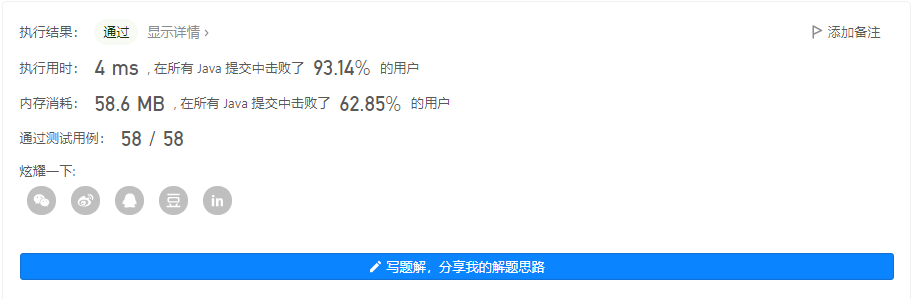
解法 2 - 二分

class Solution {
    public int findDuplicate(int[] nums) {
        // 思路：
        // 题目中要求不可以修改原数组，那么原地交换禁用
        // 二分 - [1, len - 1] 中有一个数出现了 2 次，那么每次选择一个可能的结果，判断是左边重复还是右边重复，直到边界
        // 原地交换可达到 O(n) 复杂度，而 二分复杂度为 O(nlogn) 典型的为了题意，时间换空间，实际工作中不常用
        int len = nums.length;
        return mySol(nums, 1, len - 1);
    }

    private int mySol(int[] nums, int left, int right) {
        // 递归终止条件
        if(left >= right) {
            return left;
        }
        int mid = left + ((right - left) >> 1); // 若左侧不重复且不存在缺失的数，[1, mid] 理应有 mid 个数
        int count = 0;
        for(int i : nums) {
            if(i <= mid) {
                count ++;
            }
        }
        // System.out.println(left + "  " + right + "  " + mid + "  " + count);
        if(count == mid) {
            // 左侧不重复，往右侧找
            return mySol(nums, mid + 1, right);
        } else if(count < mid){
            // 左侧不重复，但存在缺失，即某个数不止出现了 2 次，可能出现多次，但还是要往右边找
            return mySol(nums, mid + 1, right);
        } else {
            return mySol(nums, left, mid);
        }
    }
}

---

输出 2

---

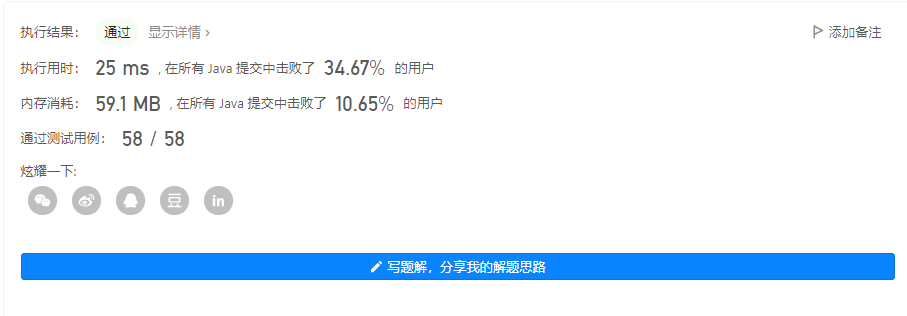
解法3 - 转换为环形链表问题

class Solution {
    public int findDuplicate(int[] nums) {
        // 思路：
        // 假设 [3, 1, 3, 4, 2] 
        // 通过 下标 -> 值 的方式串成链表，即
        // 0 -> 3
        // 1 -> 1
        // 2 -> 3
        // 3 -> 4
        // 4 -> 2
        // 那么链表连接顺序为 
        // 3 -> 4 -> 2 -> 3 形成了以 3 为环入口的环，入口环的值就是重复的元素值
        int len = nums.length; // [1, len - 1]
        // 快慢指针找环
        int slow = 0;
        int fast = 0;
        while(true) {
            slow = nums[slow];
            fast = nums[fast];
            fast = nums[fast];
            if(fast == slow) {
                break;
            }
        }
        // System.out.println(fast + "  " + slow);
        // x == z 说明从相遇位置开始走到环入口的距离 == 从起始点开始走到环入口的距离
        slow = 0;
        while(fast != slow) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
}

---

输出 3