🌕 🌗 73. 矩阵置零

难度: 🌕 🌗

问题描述

---

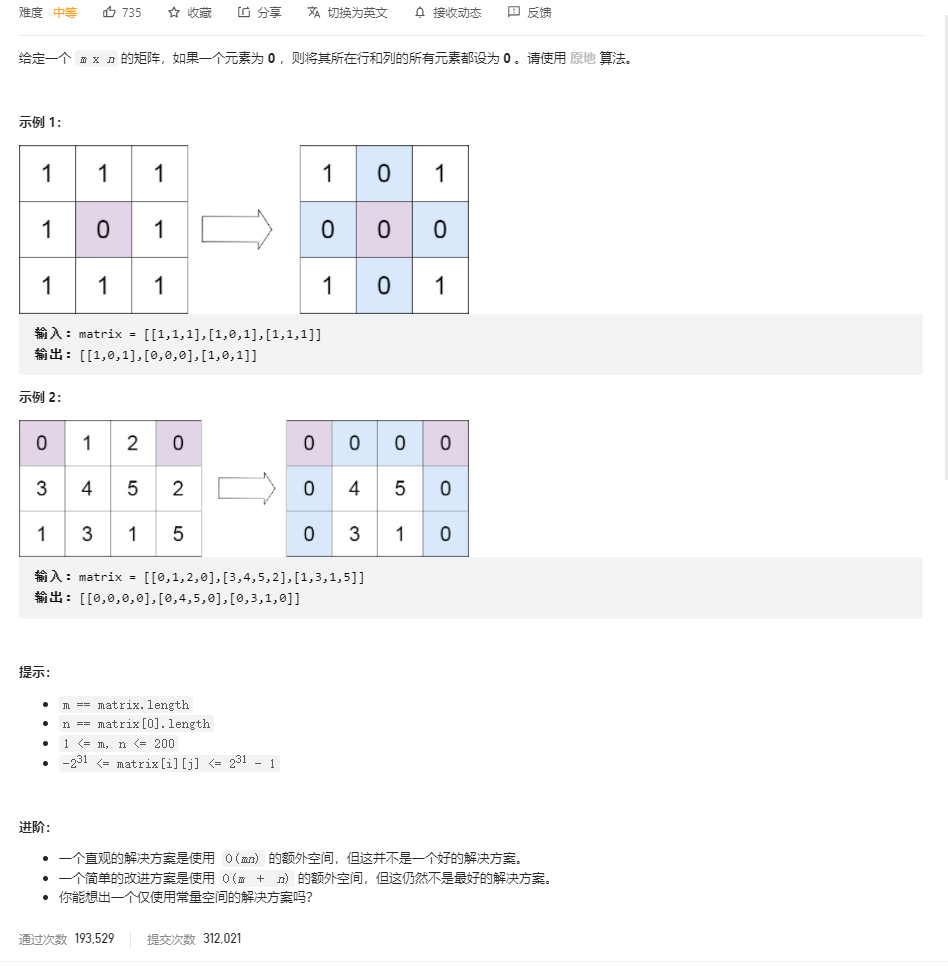
解法 1 - O(m + n)

class Solution {
    public void setZeroes(int[][] matrix) {
        // 思路：
        // method 1 - O(m + n)
        int row = matrix.length;
        int col = matrix[0].length;
        int[] rowArr = new int[col];
        int[] colArr = new int[row];
        for(int i = 0; i < row; i ++) {
            for(int j = 0; j < col; j ++) {
                if(matrix[i][j] == 0) {
                    rowArr[j] = 1;
                    colArr[i] = 1;
                }
            }
        }
        for(int i = 0; i < row; i ++) {
            for(int j = 0; j < col; j ++) {
                if(rowArr[j] == 1 || colArr[i] == 1) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

---

输出 1

---

解法 2 - O(1)

class Solution {
    public void setZeroes(int[][] matrix) {
        // 思路：
        // 借助  2 个变量，分别记录第 0 行 & 第 0 列是否存在 0
        // 若 第 0 行存在 0，则之后第 0 行全部元素 == 0
        // 记录 2 个标志位后，就可借助原 第 0 行 & 第 0 列作为之前的行数组 & 列数组，记录该行 | 该列是否应该 == 0
        // 假设 [0, 1] == 0 & 第一列其他元素均非 0 ，则 [0, 1] 仍然 == 0
        // 那么遍历时，第一列会被置 1，而由于记录了第一行标志位 == 1，说明第一行也被置零
        // 假设 [0, 1] != 0 && [1, 1] == 0 ，则 [0, 1] 会因为 [1, 1] 置为 0
        // 那么遍历时，第一列依然会被置 1，而由于第一行标志位 == 0，说明第一行并不会被置零
        int row = matrix.length;
        int col = matrix[0].length;
        boolean row0 = false;
        boolean col0 = false;
        // 先遍历首行 & 首列
        for(int j = 0; j < col; j ++) {
            if(matrix[0][j] == 0) {
                row0 = true;
                break;
            }
        }
        for(int i = 0; i < row; i ++) {
            if(matrix[i][0] == 0) {
                col0 = true;
                break;
            }
        }
        // 遍历除首行 & 首列以外的元素，覆盖首行 & 首列
        for(int i = 1; i < row; i ++) {
            for(int j = 1; j < col; j ++) {
                if(matrix[i][j] == 0) {
                    matrix[0][j] = 0; 
                    matrix[i][0] = 0;
                }
            }
        }
        // 根据首行 & 首列设置的标志位，判断该行 | 该列是否应该置零
        for(int i = 1; i < row; i ++) {
            for(int j = 1; j < col; j ++) {
                if(matrix[0][j] == 0 || matrix[i][0] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        // 根据之前的 2 个标志位，判断首行 | 首列是否该被置零
        if(row0) {
            for(int j = 0; j < col; j ++) {
                matrix[0][j] = 0;
            }
        }
        if(col0) {
            for(int i = 0; i < row; i ++) {
                matrix[i][0] = 0;
            }
        }
    }
}

---

输出 2