🌕 🌗 347. 前 K 个高频元素

难度: 🌕 🌗

问题描述

---

解法 1 - HashMap + PriorityQueue

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 思路：
        // 遍历计算各个值出现的频次
        // 排序 
        // method 1 - 借助小根堆
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i : nums) {
            if(!map.containsKey(i)) {
                map.put(i, 1);
            } else {
                int count = map.get(i);
                count ++;
                map.put(i, count);
            }
        }
        // 构造小根堆 - 自定义排序器
        PriorityQueue<Integer> queue = new PriorityQueue<>((a, b) -> {
            return map.get(a) - map.get(b);
        });
        for(int key : map.keySet()) {
            if(queue.isEmpty() || queue.size() < k) {
                queue.offer(key);
            } else {
                // 堆已满
                int peekKey = queue.peek();
                int peekVal = map.get(peekKey);
                if(map.get(key) > peekVal) {
                    queue.poll(); // 弹出一个拥有最小频次的 key
                    queue.offer(key);
                }
            }
        }
        int[] res = new int[k];
        int index = 0;
        while(!queue.isEmpty()) {
            res[index] = queue.poll();
            index ++;
        }
        return res;
    }
}

---

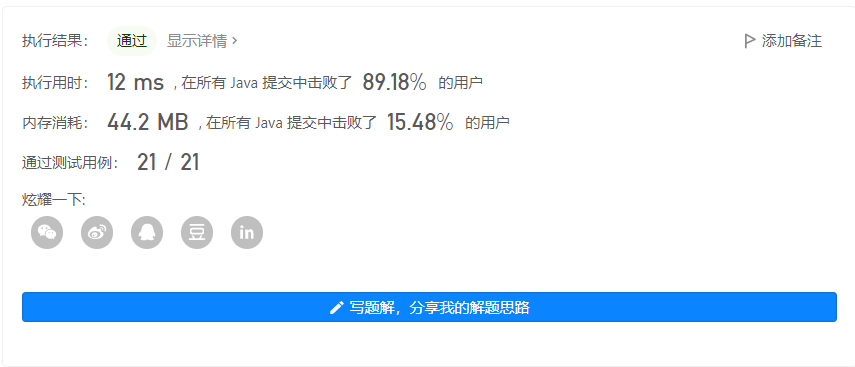
输出 1

---

解法 2 - HashMap + 桶排序

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 思路：
        // 遍历计算各个值出现的频次
        // 排序 
        // method 2 - 桶排序
        // 桶最大数量 == len + 1，将特定频次的值放在特定桶里面
        // 可遍历时记录最大频次，缩小桶的容量
        HashMap<Integer, Integer> map = new HashMap<>();
        int maxCount = 0;
        for(int i : nums) {
            if(!map.containsKey(i)) {
                map.put(i, 1);
                maxCount = Math.max(maxCount, 1);
            } else {
                int count = map.get(i);
                count ++;
                map.put(i, count);
                maxCount = Math.max(maxCount, count);
            }
        }
        // 构造桶
        List<Integer>[] buckets = new ArrayList[maxCount + 1];
        for(Map.Entry<Integer, Integer> entry : map.entrySet()) {
            int key = entry.getKey();
            int index = entry.getValue();
            if(buckets[index] == null) {
                List<Integer> list = new ArrayList<>();
                list.add(key);
                buckets[index] = list;
            } else {
                List<Integer> list = buckets[index];
                list.add(key);
                buckets[index] = list;
            }
        }
        int[] res = new int[k];
        int index = 0;
        for(int i = buckets.length - 1; i >= 0; i --) {
            if(buckets[i] != null) {
                List<Integer> list = buckets[i];
                for(int j = 0; j < list.size(); j ++) {
                    res[index] = list.get(j);
                    index ++;
                    if(index == k) {
                        return res;
                    }
                }
            }
        }
        return res;
    }
}

---

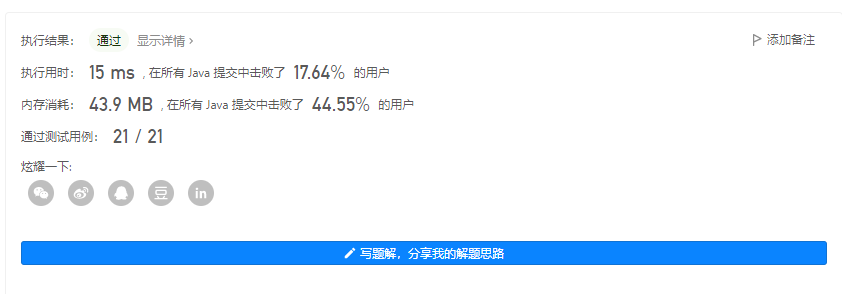
输出 2

---

解法 3 - HashMap + 变形快排

class Solution {
    int k;
    public int[] topKFrequent(int[] nums, int k) {
        // 思路：
        // 获得 [val, fre] 之后，进行快排
        // 单方向递归，将复杂度降到 O(N)
        this.k = k;
        HashMap<Integer, Integer> map = new HashMap<>(); // 统计 val - fre
        for(int i: nums) {
            if(!map.containsKey(i)) {
                map.put(i, 1);
            } else {
                int fre = map.get(i);
                fre ++;
                map.put(i, fre);
            }
        }
        // 填充新的数据结构 - 含 val - fre
        int len = map.size();
        int[][] arr = new int[len][2];
        int index = 0;
        for(Map.Entry<Integer, Integer> entry: map.entrySet()) {
            int val = entry.getKey();
            int fre = entry.getValue();
            arr[index] = new int[]{val, fre};
            index ++;
        }
        // 快排
        int[] res = new int[k];
        mySol(arr, len, 0, len - 1, 0, res);
        return res;
    }

    private void mySol(int[][] arr, int len, int left, int right, int index, int[] res) {
        // 递归终止条件
        if(left >= right) {
            res[index] = arr[left][0];
            index ++;
            return;
        }
        // left < right
        int monitor = arr[left][1]; // 比较的是频次，频次比它小的放到左边，大的放到右边
        int i = left;
        int j = right;

        while(i < j) {
            while(i < j && arr[j][1] >= monitor) {
                j --;
            }
            while(i < j && arr[i][1] <= monitor) {
                i ++;
            }
            swap(arr, i, j);
        }
        swap(arr, left, i);
        // 判断接下来继续快排那一边
        // 当前需要填充的下标是 index，则还有 k - 1 - index + 1 = k - index 个元素需要填充
        // 若正好 [i, right] 元素有 k - index 个，即
        // right - i + 1 = k - index ==> i = right + index - k + 1
        if(i == right + index - k + 1) {
            for(int m = i; m <= right; m ++) {
                res[index] = arr[m][0];
                index ++;
            }
        } else if(right - i + 1 > k - index) {
            // 右侧比 monitor 频次大的数比想要的多，因此右侧还需继续快排
            mySol(arr, len, i + 1, right, index, res);
        } else {
            // 右侧比 monitor 频次大的数比想要的少，说明右侧所有数均要加入结果集，然后左侧还需继续填充部分到结果集中
            for(int m = i; m <= right; m ++) {
                res[index] = arr[m][0];
                index ++;
            }
            mySol(arr, len, left, i - 1, index, res);
        }
    }

    private void swap(int[][] arr, int a, int b) {
        int[] tmp = arr[a];
        arr[a] = arr[b];
        arr[b] = tmp;
    }
}

---

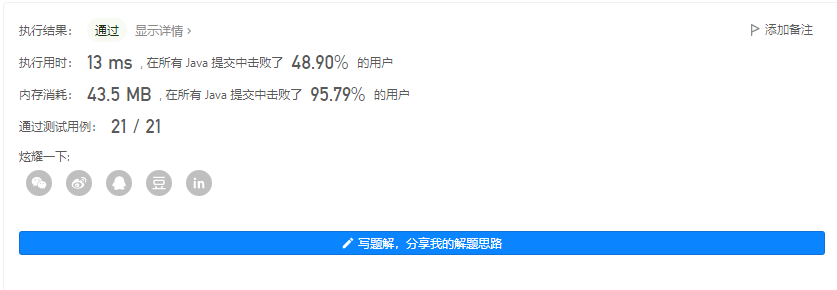
输出 3