🌕🌕 352. 将数据流变为多个不相交区间

难度: 🌕🌕

问题描述

---

解法 1 - TreeSet

class SummaryRanges {
    // 思路：
    // 以 [from, to] 为一个整体添加
    // 添加 val 时，能快速找到 前一个区间 prev[] & 后一个区间 next[]
    // 判断能否与 prev | next 合并，如果能合并，需要调整 区间边界，如何 prev & next 均能合并，还需要删除一个区间
    // 获取所有不想交区间时，能快速遍历
    // 这个数据结构能想到的就是 TreeSet - 有序集合

    TreeSet<int[]> set = new TreeSet<>((a, b) -> {
        return a[0] - b[0]; // 升序
    });
    int[] head = new int[]{-10, -10}; // 由于有 边界值 + 1 这个范围，因此不好直接使用 -1 填充 head，找一个肯定不会与任何值何必的值，例 10
    int[] tail = new int[]{10010, 10010}; // 由于题意中 val 范围限定，因此可以添加虚拟哨兵节点，防止查找到 null

    public SummaryRanges() {
        set.add(head);
        set.add(tail);
    }
    
    public void addNum(int val) {
        int[] cur = new int[]{val, val};
        int[] prev = set.floor(cur); // 前面一个区间
        int[] next = set.ceiling(cur); // 后一个区间
        // System.out.println(Arrays.toString(prev) + " " + val + " " + Arrays.toString(next));
        // 分情况讨论 - prev[], next[] --> val 存在 5 个位置
        // 新区间
        if(val > prev[1] + 1 && val < next[0] - 1) {
            set.add(cur);
            return; 
        }
        // 处于 prev[] | next[] 区间范围内，和任意一个区间合并
        if(val == prev[1] + 1 && val < next[0] - 1) {
            prev[1] ++;
            return;
        }
        if(val > prev[1] + 1 && val == next[0] - 1) {
            next[0] --;
            return;
        }
        // 和 prev[] & next[] 均合并
        if(val == prev[1] + 1 && val == next[0] - 1) {
            prev[1] = next[1];
            set.remove(next);
        }
    }
    
    public int[][] getIntervals() {
        // 遍历 set
        int len = set.size();
        Iterator<int[]> ite = set.iterator();
        ite.next(); // 去掉虚拟头节点
        int[][] res = new int[len - 2][2];
        int index = 0;
        while(index < len - 2) {
            res[index] = ite.next();
            index ++;
        }
        return res;
    }
}

/**
 * Your SummaryRanges object will be instantiated and called as such:
 * SummaryRanges obj = new SummaryRanges();
 * obj.addNum(val);
 * int[][] param_2 = obj.getIntervals();
 */

---

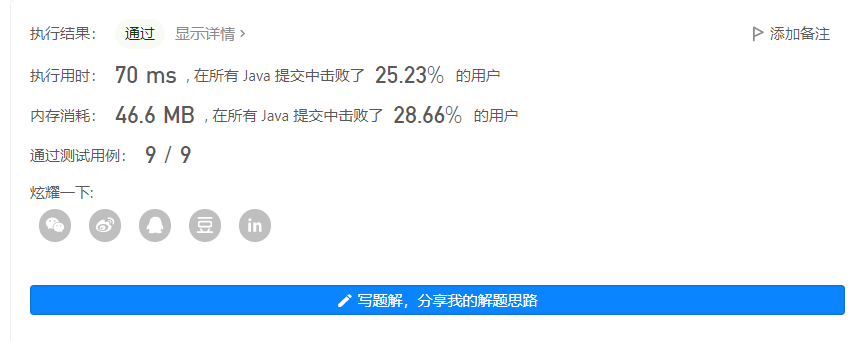
输出 1

---

解法 2 - 并查集

class SummaryRanges {
    // 思路：
    // 并查集
    // 由于 val ∈ [0, 10000] ∴ 可以用数组标记每一位是否存在值，若存在，标记为 true
    // 通过并查集，得到 该下标处对应的父亲下标，即右边界
    // 在获取不相交区间时，可以遍历数组得到
    // 为提高速度，可通过 TreeSet 记录所有的左边界，这样就无需找到某个右边界后，依次向后查找下一个左边界
    TreeSet<Integer> set; // 只记录左边界
    int[] arr; // 判断下标处是否有值
    int len = 10001;

    public SummaryRanges() {
        set = new TreeSet<>();
        arr = new int[len];
        // 初始化，起初所有下标处的父亲均设置为 -1，表示没有右边界
        Arrays.fill(arr, -1);
    }
    
    public void addNum(int val) {
        if(arr[val] != -1) {
            return; // 说明该值已经添加过，这一点很重要
        }
        set.add(val);
        arr[val] = val;
        // 连接同右节点
        union(val - 1, val); // 和左区间判断是否能够合并
        union(val, val + 1);
    }

    private int getFather(int index) {
        if(arr[index] != index) {
            return getFather(arr[index]);
        } else {
            return index;
        }
    } 
    private void union(int from, int to) {
        // 将 from 和 to 连接到同一个父亲
        // 区别于普通并查集在于，需要判断是否为 -1，若为 -1，说明没有该节点，那么无法进行连接
        if(from < 0 || to >= len || arr[from] == -1 || arr[to] == -1) {
            return;
        }
        int ff = getFather(from);
        int ft = getFather(to);
        if(ff >= ft) {
            return; // 说明 from 能到达的连续区间右边界已经包含了 to 的右边界
        }
        arr[from] = ft;
        // 从 set 中去掉 to，说明 to 不是左边界
        set.remove(to);
    }
     
    public int[][] getIntervals() {
        int size = set.size(); // 从 set 中获取左边界
        int[][] res = new int[size][2];
        int index = 0;
        for(int i: set) {
            res[index] = new int[]{i, getFather(i)};
            index ++;
        }
        return res;
    }
}

/**
 * Your SummaryRanges object will be instantiated and called as such:
 * SummaryRanges obj = new SummaryRanges();
 * obj.addNum(val);
 * int[][] param_2 = obj.getIntervals();
 */

---

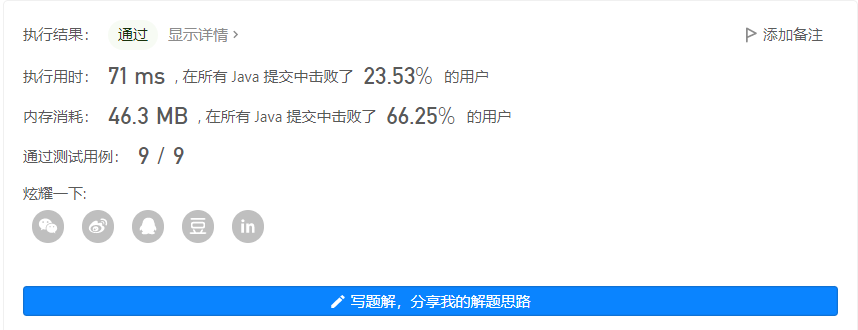
输出 2