🌕🌗 373. 查找和最小的 K 对数字

难度: 🌕🌗

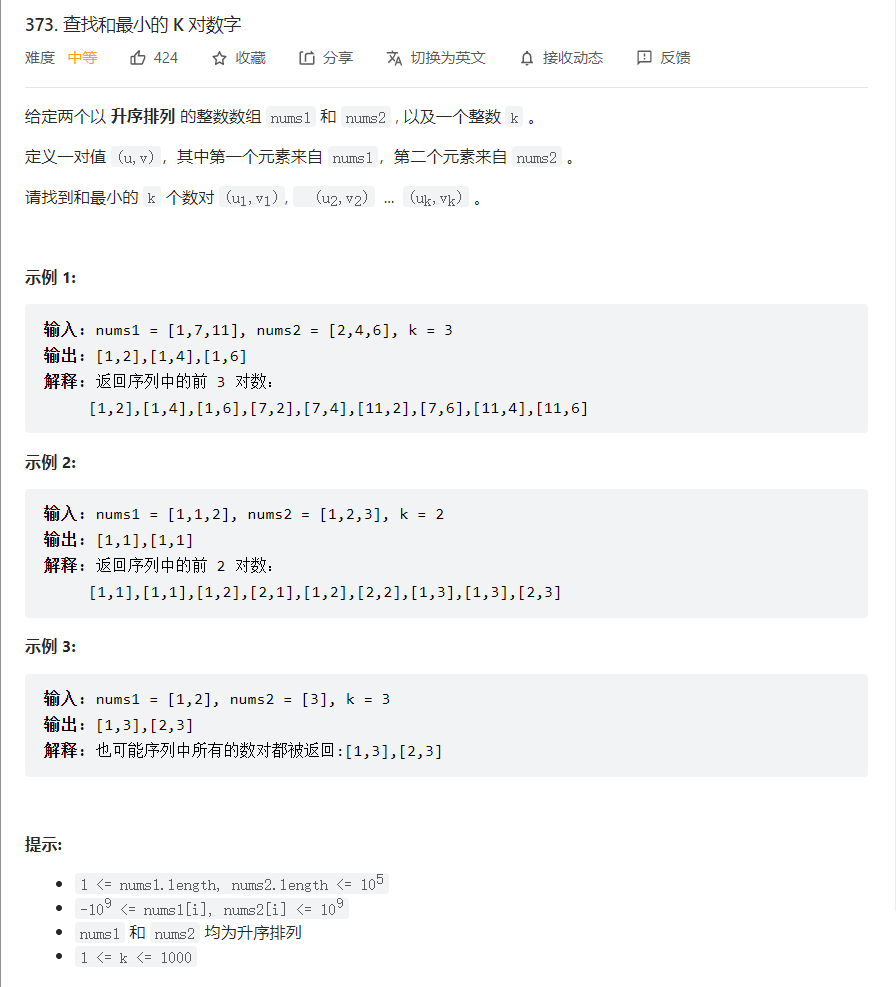
问题描述

---

解法

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        // 思路：
        // 首先想到的是双指针，根据 cur 确定 next 对应的下标，但这样存在一个问题
        // 假设 cur 时对应 i, j, next 时 对应 i + 1, j
        // 那么 next 后面的 fur 只能是 i + 1, j 之后的指针，但也许寻找一种情况，实际想要的 fur 为 i, j + 1
        // 由于指针不能后退，因此出现了错误
        // 修改思路，一共有如下情况
        // 1[0] + 2[0], 1[0] + 2[1], ..., 1[0] + 2[n - 1]
        // 1[1] + 2[0], 1[1] + 2[1], ..., 1[1] + 2[n - 1]
        // ...
        // 1[m - 1] + 2[0], 1[m - 1] + 2[1], ..., 1[m - 1] + 2[n - 1]
        // 这样就转换为了 优先堆问题，每次放入堆顶元素，取出后，如果还存在后续元素，继续入队
        int m = nums1.length;
        int n = nums2.length;

        // m <= n
        List<List<Integer>> res = new ArrayList<>();
        // 堆顶元素应该最小 - 小根堆 - 升序
        PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> {
            return nums1[a[0]] + nums2[a[1]] - (nums1[b[0]] + nums2[b[1]]);
        });
        // 初始情况入队
        for(int i = 0; i < Math.min(m, k); i ++) {
            queue.offer(new int[]{i, 0}); // nums[2] 初始下标为 0
            // System.out.println(i + " : " + "0");
        }
        int count = 0;
        while(count < k && !queue.isEmpty()) {
            int[] cur = queue.poll();
            int x = cur[0];
            int y = cur[1];
            ArrayList<Integer> list = new ArrayList<>();
            list.add(nums1[x]);
            list.add(nums2[y]);
            res.add(list);
            if(y + 1 < n) {
                y ++;
                queue.offer(new int[] {x, y});
                // System.out.println(x + " : " + y);
            }
            count ++;
        }
        return res;
    }
}

---

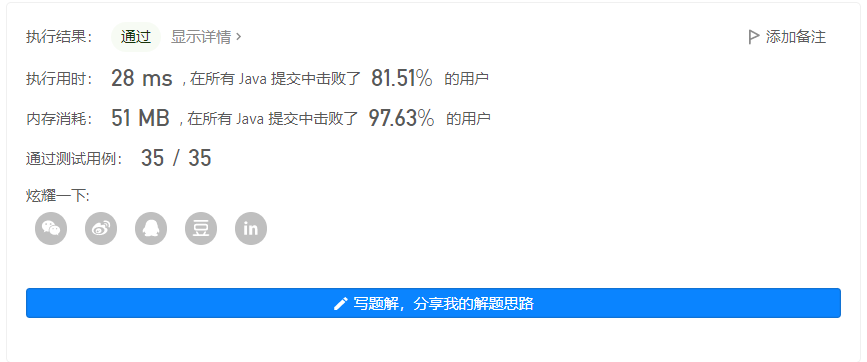
输出