🌕 42. 接雨水

难度: 🌕

问题描述

---

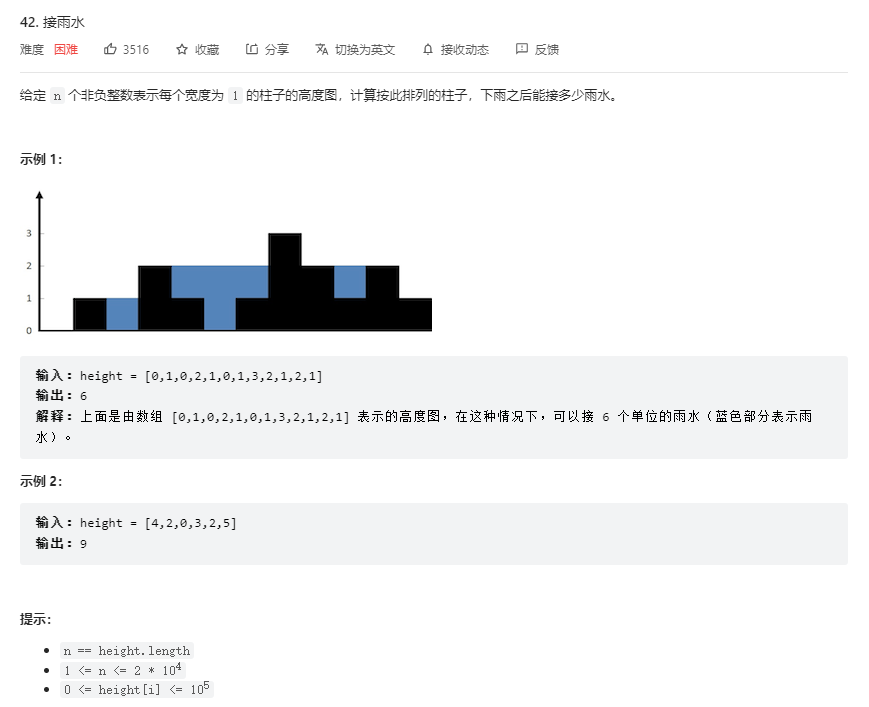
解法 1 - 单向遍历

class Solution {
    public int trap(int[] height) {
        // 思路：
        // 竖着相加，求每个下标处能接多少雨水
        // 每个下标处可接雨水，取决于该下标两侧的最大值 & 自身高度
        // 左右两边较小值 - 自身高度 即为该处可接雨水量
        // 左右添加哨兵节点 0 方便运算
        int len = height.length;
        int[] left = new int[len];
        int[] right = new int[len];
        // 从左到右遍历，求左侧最大值
        int leftMax = 0;
        for(int i = 1; i < len; i ++) {
            leftMax = Math.max(leftMax, height[i - 1]);
            left[i] = leftMax;
        }
        // 从右到左遍历，求右侧最大值
        int rightMax = 0;
        for(int j = len - 2; j >= 0; j --) {
            rightMax = Math.max(rightMax, height[j + 1]);
            right[j] = rightMax;
        }
        // 最后一次遍历，求每个下标处能接的雨水
        int res = 0;
        for(int i = 0; i < len; i ++) {
            int min = Math.min(left[i], right[i]);
            if(height[i] < min) {
                res += (min - height[i]);
            }
        }
        return res;
    }
}

---

输出 1

---

解法 2 - 单调栈

class Solution {
    public int trap(int[] height) {
        // 思路：
        // 单调栈 - 构造 非严格递减栈
        // 画图就出来了
        int len = height.length;
        LinkedList<Integer> stack = new LinkedList<>();
        int res = 0;
        for(int i = 0; i < len; i ++) {
            if(stack.isEmpty()) {
                stack.push(i);
            } else {
                // stack 非空
                int cur = height[i];
                int tmpPeek = height[stack.peek()];
                if(cur < tmpPeek) {
                    stack.push(i);
                } else if(cur == tmpPeek) {
                    // 替换原节点，下标更正为 ++
                    stack.pop();
                    stack.push(i);
                } else {
                    // 需要取出元素，求雨水，雨水是一行行求的
                    while(!stack.isEmpty() && cur > height[stack.peek()]) {
                        int bottom = height[stack.pop()]; // 最低位
                        if(!stack.isEmpty()) {
                            // 取出当前列后，还存在左边界
                            int leftIndex = stack.peek();
                            int width = i - leftIndex - 1; // 左边界由 leftIndex 决定，而非 pop 出来的元素的下标
                            int hi = Math.min(cur, height[leftIndex]);
                            int square = width * (hi - bottom);
                            res += square;
                            // System.out.println(width + "  " + hi + "  " + bottom + "  " + square);
                        }
                    }
                    stack.push(i);
                }
            }
        }
        return res;
    }
}

---

输出 2

---

解法 3 - 优先队列

class Solution {
    public int trap(int[] height) {
        // 思路：
        // 借助 优先队列 - <下标，高度>
        // 初始压入左右边界值
        // 每次弹出较小的元素，判断能否往左右两侧注水，需要数组去重，压入左右两侧元素
        int len = height.length;
        // 特殊情况特判
        if(len <= 2) {
            return 0;
        }
        // len > 2
        int res = 0;
        int[] arr = new int[] {-1, 1}; // 左右两个方向
        boolean[] visit = new boolean[len];
        PriorityQueue<int[]> queue = new PriorityQueue<>((a, b) -> {
            return a[1] - b[1]; // 根据高度建立小根堆
        });
        // 压入左右两侧元素
        queue.offer(new int[] {0, height[0]});
        queue.offer(new int[] {len - 1, height[len - 1]});
        visit[0] = true;
        visit[len - 1] = true;
        // 循环
        while(!queue.isEmpty()) {
            int[] cur = queue.poll();
            // 初始门票：
            // 边界值有效 && 没有被访问过
            // 成功注水门票：
            // 高度 < cur[1]
            for(int j: arr) {
                int index = cur[0] + j;
                if(index >= 0 && index < len && !visit[index]) {
                    if(height[index] < cur[1]) {
                        res += cur[1] - height[index]; // 可以往左 | 右 方向注水，使之达到当前最小高度
                        queue.offer(new int[] {index, cur[1]}); // 注水后高度为 cur[1]
                    } else {
                        // 无需注水，压入实际高度
                        queue.offer(new int[] {index, height[index]});
                    }
                    visit[index] = true;
                } 
            }
        }
        return res;
    }
}

---

输出 3