🌕 295. 数据流的中位数

难度: 🌕

问题描述

---

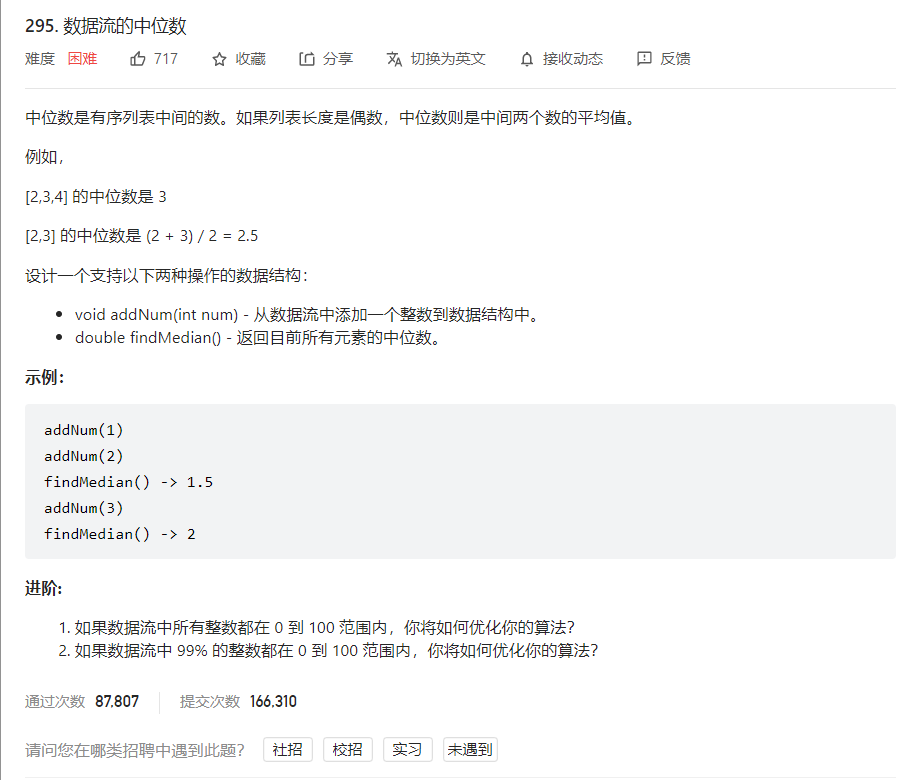
解法

class MedianFinder {
    // 思路：
    // 双优先队列 - 保证查复杂度 O(1)
    // 始终保证中位数不是 left 堆顶，就是 left & right 堆顶平均值
    PriorityQueue<Integer> left; 
    PriorityQueue<Integer> right;

    public MedianFinder() {
        left = new PriorityQueue<>((a, b) -> {
            return b - a;
        });
        right = new PriorityQueue<>((a, b) -> {
            return a - b; // 不重写也可以，默认小根堆
        });
    }
    
    public void addNum(int num) {
        int llen = left.size();
        int rlen = right.size();
        if(llen == 0) {
            left.offer(num);
            return;
        }
        // llen > 0 && rlen > 0
        if(llen == rlen) {
            // 需要在 left 添加元素
            if(num <= right.peek()) {
                left.offer(num);
            } else {
                // 从 right 弹出堆顶元素放入 left，将 num 放入 right
                int tmp = right.poll();
                left.offer(tmp);
                right.offer(num);
            }
        } else {
            // 需要在 right 添加元素，添加后 两个队列元素相等
            if(num >= left.peek()) {
                right.offer(num);
            } else {
                // 从 left 弹出一个元素放入 right， 将 num 放入 left
                int tmp = left.poll();
                right.offer(tmp);
                left.offer(num);
            }
        }
    }
    
    public double findMedian() {
        int llen = left.size();
        int rlen = right.size();
        if(llen == rlen) {
            return (double)(left.peek() + right.peek()) / 2;
        } else {
            return (double) left.peek();
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

---

输出

---

进阶 1

• 桶排序，维护 101 个桶

---

进阶 2

• 在 [0, 100] 维护 101 个桶
• 在区间外
  • 另外维护 2 个数组
    • 若中位数在 [1, 100] 之间，同 进阶 1
    • 若特殊情况下，中位数在 两边，排序暴搜
  • 维护有序集合 TreeMap
    • 特殊情况下，中位数在 两边时，快速定位中位数