🌕 342. 4的幂

难度: 🌕

问题描述

---

解法 1

class Solution {
    public boolean isPowerOfFour(int n) {
        // 思路：
        // 4 的幂 说明 一定是 2 的幂
        // 首先验证是否为 2 的幂
        // 如何验证是否为 2 的幂？
        // 借助 x & (x - 1) 消去 1 个 0 后判断是否为 0 得出
        // 然后判断是否为 4 的幂
        // 可以看出，4 的幂 二进制为 0001 每次左移 2 位
        // 也就是说，二进制偶数位上有且只有一个 1，奇数位全为 0
        // ∴ 可以构造一个数，使得 x 与这个数想与能够区分出 这个唯一的 1 到底在 奇数位还是 偶数位
        // 一个可能的数可以表示为 (0101) * 8 = 8 个 5
        // x & (5555 5555) != 0 说明 1 在偶数位上，即是 4 的幂
        // 另一个可能的数可以表示为 (1010) * 8 = 8 个 A
        // x & (AAAA AAAA) != 0 说明 1 在奇数位上，即不是 4 的幂
        if(n < 1) {
            return false;
        }
        if((n & (n - 1)) != 0) {
            return false;
        }
        int monitor = 0xAAAAAAAA;
        if((n & monitor) != 0) {
            return false;
        } else {
            return true;
        }
    }
}

---

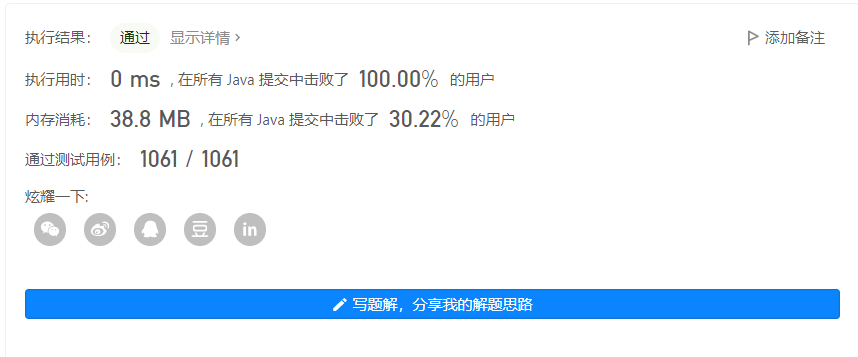
输出 1

---

解法 2

class Solution {
    public boolean isPowerOfFour(int n) {
        // 思路：
        // 还是首先判断是否为 2 的幂
        // 4^x = (3 + 1)^x 展开后除去 3 的乘积，最终只剩下 1 这个余数
        // 即 (4^x) % 3 == 1
        // 若为 2 的幂但不是 4 的幂，则
        // 2 * 4^x = 2 * 4 * 4^(x - 1) = 8 * 4^(x - 1)
        // 则 8 * 4^(x - 1) % 3 = 8 % 3 * 1 = 2
        if(n < 1) {
            return false;
        }
        if((n & (n - 1)) != 0) {
            return false;
        }
        return n % 3 == 1;
    }
}

---

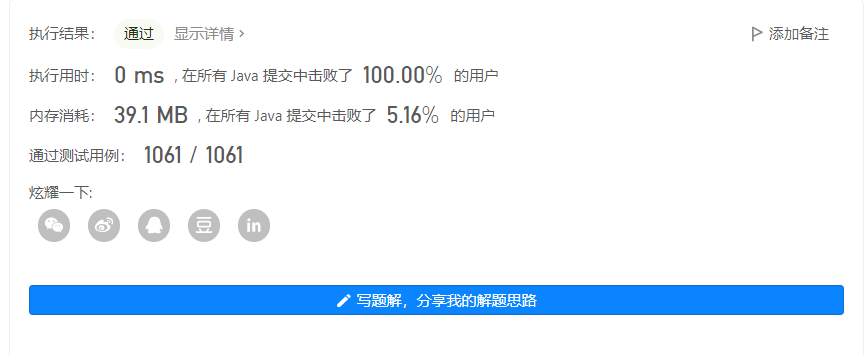
输出