🌕🌗 397. 整数替换

难度: 🌕🌗

问题描述

---

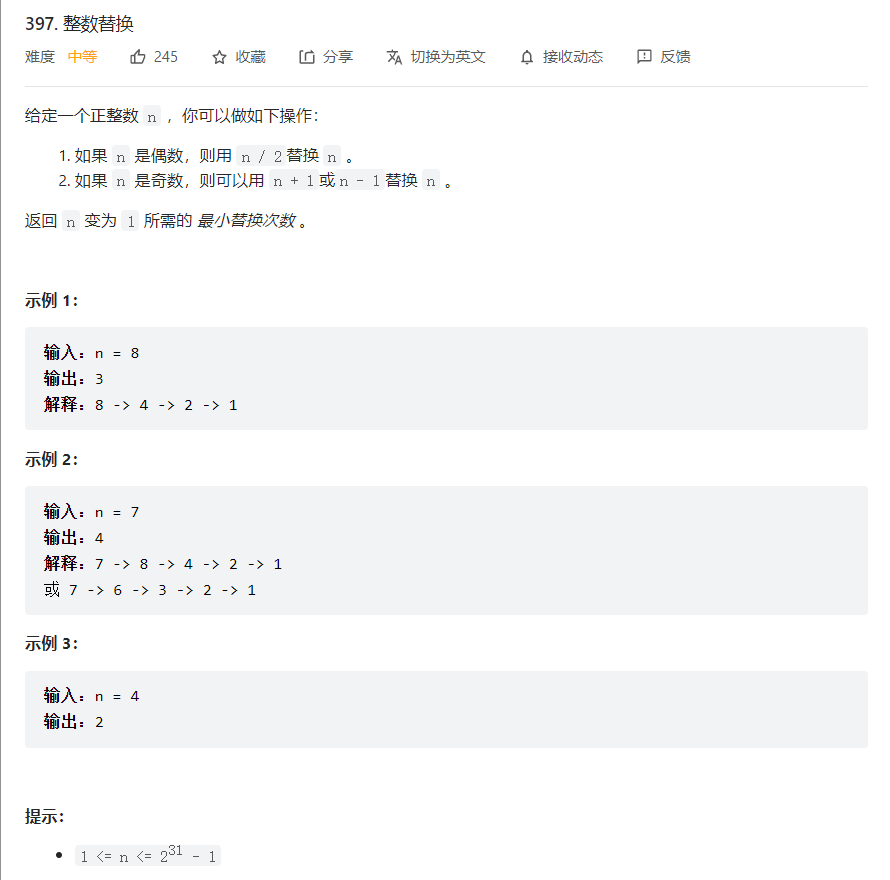
解法 1 - dp[超内存]

class Solution {
    public int integerReplacement(int n) {
        // 思路：
        // dp
        if(n == 1) {
            return 0;
        }
        // 要考虑到如果 n 为奇数，那么 dp[n + 1] 还需要计算到，因此最多计算到 dp[n + 1]
        int[] dp = new int[n + 2];
        dp[1] = 0;
        dp[2] = 1;
        // 两个两个计算，先计算后面的偶数
        for(int i = 3; i + 1 < n + 2; i = i + 2) {
            dp[i + 1] = dp[(i + 1) / 2] + 1;
            dp[i] = Math.min(dp[i - 1], dp[i + 1]) + 1;
        }
        return dp[n];
    }
}

---

解法 2 - 递归 + map

class Solution {
    HashMap<Long, Integer> map = new HashMap<>();
    public int integerReplacement(int n) {
        // 思路：
        // 递归
        // 单独递归当用例为 2147483647 时，仍会造成栈溢出
        // 因此还需要再进行优化
        // 引入 map 存储已经计算的值，降低复杂度
        return mySol(n);
    }

    private int mySol(long cur) {
        // 递归终止条件
        if(cur == 1) {
            return 0;
        }
        if(map.containsKey(cur)) {
            return map.get(cur);
        } 
        int res = 0;
        if((cur & 1) == 1) {
            // 奇数
            res = Math.min(mySol(cur - 1), mySol(cur + 1)) + 1;
        } else {
            // 偶数
            res = mySol(cur / 2) + 1;
        }
        map.put(cur, res);
        return res;
    }
}

---

输出 2

---

解法 3 - 位运算

class Solution {
    public int integerReplacement(int n) {
        // 思路：
        // 找规律
        // 当 n 为奇数时，到底是 n + 1 还是 n - 1 这个操作是确定的
        // 假设 n 的最低位为 xx01，那么
        // n + 1 --> xx10 --> xxx1
        // n - 1 --> xx00 --> xxx0
        // 可以看出，我们要做的就是尽可能将 n 的 最低位的 1 消去，当然最后一步的 2 |3 除外，我们需要保留其最低位的 1
        // 当 n 的最低位为 xx01 时，执行 ++ 不能导致 1 的消除，至少移到了前一位，这个 1 最终还是要被处理掉
        // 执行 -- 时，消去了最低位的 1 因此步骤较少，此时采用 --
        // 当 n 的最低位位 xx11 时，执行 ++ 至少能够消去 1 个 1
        // 执行 -- 只能消去一个 1，因此对于最低位非 xx01 的情况，采用 ++，尽可能多的消去 1
        // 特殊情况：
        // n == 3 即 n == 0011 时，
        // 若执行 ++，变为 0100 --> 0010 --> 0001 需要经过 3 步
        // 若执行 --，变为 0010 --> 0001 需要经过 2 步
        if(n == 1) {
            return 0;
        }
        // 反正超范，转换为 long
        long cur = n;
        int res = 0;
        while(cur != 1) {
            if((cur & 1) == 0) {
                // 偶数
                cur /= 2;
                res ++;
            } else {
                // 奇数 - 判断最低位是否只有一个 1
                if((cur & 2) == 0 || cur == 3) {
                    // 只有一个 1
                    cur --;
                    res ++;
                } else {
                    // 不止 一个 1
                    cur ++;
                    res ++;
                }
            }
        }
        return res;
    }
}

---

输出 3