🌕🌕🌗 400. 第 N 位数字

难度: 🌕🌕🌗

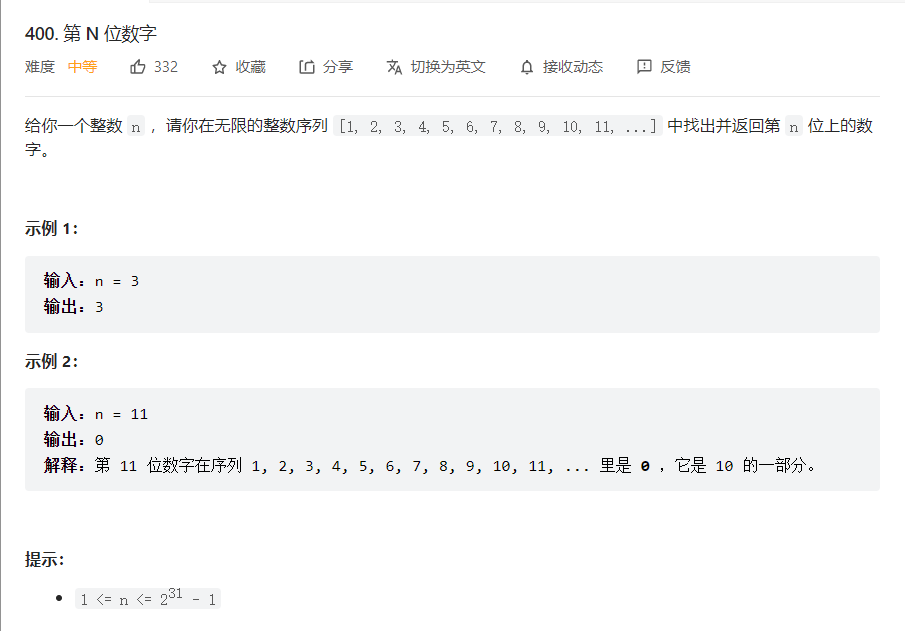
问题描述

---

解法

class Solution {
    public int findNthDigit(int n) {
        // 思路：
        // 找规律
        // 一位数时，共有 9 个数，起始值为 1, 占 9 位
        // 两位数时，共有 90 个数，起始值为 10, 占 180 位
        // 三位数时，共有 999 - 100 + 1 = 900 个数，占 900 * 3 位
        // n 位数时，共有 9 * 10^(n - 1) * n 位数
        // 因此首先可以确定 n 属于多少位数 x， 得到该位数起始值 10^x
        // 再次确定 n 位于该位数的第多少位 n - 前面几位占用的位数
        // 根据 除数 - 1 得到目标值，根据 余数 得到目标值的第多少位
        if(n <= 9) {
            return n;
        }

        long num = n;
        long prev = 0; // 前面几位全部所占的位数
        int len = 1; // 当前是几位数
        long cur = 9 * (int)Math.pow(10, len - 1) * len; // 当前轮全部包含所占的位数
        while(num > prev + cur) {
            // 说明当前轮所在的位数不是目标值所在位数，还需要继续增加位数
            prev += cur;
            len ++;
            cur = 9 * (long)Math.pow(10, len - 1) * len;
        }
        // System.out.println(prev + "  len: " + len + " cur: " + cur);
        // 确定当前位数，计算偏移量
        int orig = (int)Math.pow(10, len - 1); // 该位数的初始值
        int count = n - (int)prev - 1; // 针对该位数初始值的下标，从 0 开始
        int offset = count / len; // 相对于该位数起始值的偏移量
        int real = orig + offset; // 该位数所在的实际值
        System.out.println(real);
        int index = count % len; // 在该位数下针对于最高位的偏移量 - 从 0 开始
        String str = String.valueOf(real); // 转换为字符串后可以方便得到第 index 位所在的值
        return (int)(str.charAt(index) - '0');
    }
}

---

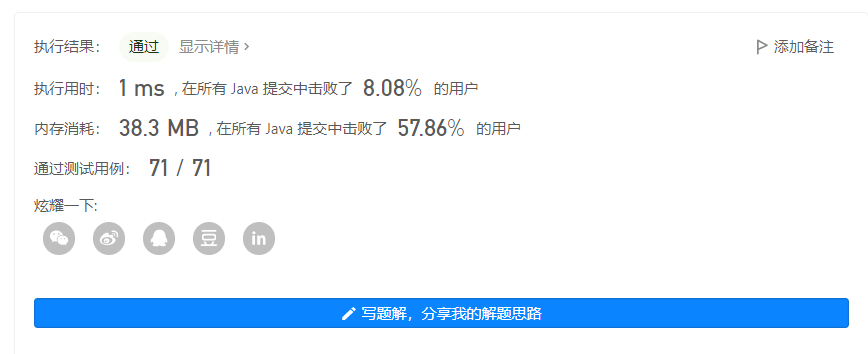
输出