🌕🌕🌗 149. 直线上最多的点数

难度: 🌕🌕🌗

问题描述

---

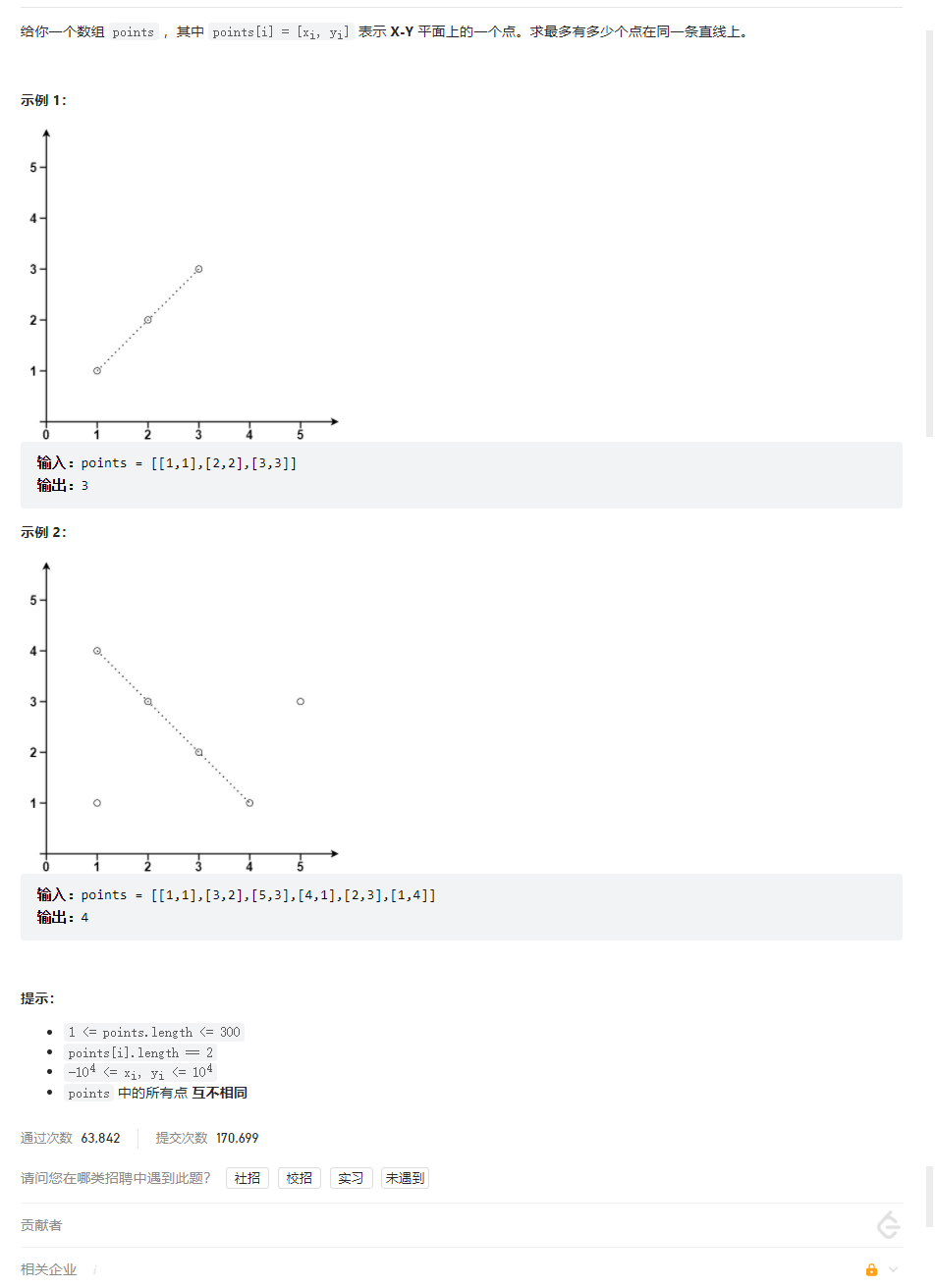
解法

class Solution {
    public int maxPoints(int[][] points) {
        // 思路：
        // 固定一个端点，借助 HashMap 存储所有可能的斜率 & 对应的点集合
        // 可以优化的点如下：
        // 1. 若某个斜率下的点个数 > len / 2 说明剩下的点即使全部在另一条直线上，也不可能比这条集合的点多
        // 此时可以只考虑剩下的节点是否能在当前斜率下处于同一条直线，其他斜率不用考虑
        // 
        // 斜率如何记录？
        // 由于 double 也可能出现截断造成不相等的情况，可以通过该斜率下已经存在的两点 [ax, ay] & [bx, by]
        // 针对当前节点 [x, y] 满足条件 (by - ay) / (bx - ax) = (y - ay) / (x - ax)
        // 整理得，(by - ay) * (y - ax) == (y - ay) * (bx - ax)
        // 即使如此，map 的 key 仍需要保存一个斜率，可以将其尽量转换为整数
        // x, y ∈ [-10^4, 10^4] 说明，△x, △y ∈ [-2 * 10^4, 2 * 10^4]
        // 进而，△y / △x ∈ [-1/(2 * 10^4), 2 * 10^4]
        // 从而，可以对 斜率 * (2 * 10^4) 保证斜率转换为整数
        int len = points.length;
        // 特殊情况特判
        if(len == 1) {
            return 1;
        }
        if(len == 2) {
            return 2;
        }
        // len > 2
        int maxCount = 2;
        int max = Integer.MAX_VALUE;
        
        for(int i = 0; i < len; i ++) {
            int[] cur = points[i]; // 当前点，希望和其他点组成直线
            // 固定 cur 作为一个端口，依次遍历其他点形成直线，更新 map
            HashMap<Integer, ArrayList<int[]>> map = new HashMap<>();     
            int curCount = 2; // 以 cur 为左端点，形成直线的最大点数 
            boolean flag = false; // 是否找到最大斜率的节点，若为 true，之后只需要与该斜率判断    
            int diffY = -1; // 当 flag == true 时的右端点 - 左端点
            int diffX = -1;
            for(int j = 0; j < len; j ++) {
                if(j == i) {
                    continue; // 是自己，跳过
                }
                int[] candicate = points[j]; // 待组成直线的候选节点
                if(cur[1] > candicate[1]) {
                    continue; // cur 只和 y 值比它大的节点
                }
                if(flag) {
                    // 满足条件，只需要判断一个斜率
                    if(diffX * (candicate[1] - cur[1]) == diffY * (candicate[0] - cur[0])) {
                        curCount ++; // 只需要更新这个值，无需继续更新 map 
                    }
                    continue;
                }
                if(cur[1] == candicate[1]) {
                    // 说明是水平线
                    if(!map.containsKey(0)) {
                        ArrayList<int[]> tmpList = new ArrayList<>();
                        map.put(0, tmpList);
                    }
                    ArrayList<int[]> curList = map.get(0);
                    curList.add(candicate); // 加入候选节点
                    // 判断是否更新 curCount
                    curCount = Math.max(curCount, curList.size() + 1);
                    // 判断是否可以找到最大频率
                    if(curCount > (len / 2)) {
                        flag = true;
                        // 求 diffX & diffY
                        // 随便从 map 中该斜率下找一个其他点，为方便，直接取 candicate
                        diffX = candicate[0] - cur[0];
                        diffY = candicate[1] - cur[1];
                    }
                    continue;
                }
                if(cur[0] == candicate[0]) {
                    // 说明为垂直线
                    if(!map.containsKey(max)) {
                        ArrayList<int[]> tmpList = new ArrayList<>();
                        map.put(max, tmpList);
                    }
                    ArrayList<int[]> curList = map.get(max);
                    curList.add(candicate); // 加入候选节点
                    curCount = Math.max(curCount, curList.size() + 1);
                    if(curCount > (len / 2)) {
                        flag = true;
                        diffX = candicate[0] - cur[0];
                        diffY = candicate[1] - cur[1];
                    }
                    continue;
                }
                // 非水平 & 非垂直 线段
                int scope = (candicate[1] - cur[1]) * 20000 / (candicate[0] - cur[0]);
                // System.out.println(i + "  " + scope + "  " + curCount);
                if(!map.containsKey(scope)) {
                    ArrayList<int[]> tmpList = new ArrayList<>();
                    tmpList.add(candicate);
                    map.put(scope, tmpList);
                } else {
                    // 由于 scope 也是经过约分的，所以还需要严格判断，是否真的可以组成一条直线
                    ArrayList<int[]> curList = map.get(scope);
                    int tmpCount = 2;
                    int dx = candicate[0] - cur[0];
                    int dy = candicate[1] - cur[1];
                    for(int[] select: curList) {
                        if(dx * (select[1] - cur[1]) == dy * (select[0] - cur[0])) {
                            tmpCount ++; // 除了 cur candicate 还有其他节点可以组成
                        }
                    }
                    curCount = Math.max(curCount, tmpCount);
                    curList.add(candicate); 
                    // 判断是否更新 curCount
                    if(curCount > (len / 2)) {
                        flag = true;
                        diffX = candicate[0] - cur[0];
                        diffY = candicate[1] - cur[1];
                    }
                }
            }
            // 以 cur 为左端点，已经全部遍历完
            maxCount = Math.max(maxCount, curCount);
            // System.out.println(i + "  " + curCount);
            // 特殊情况判断
            if(maxCount == len) {
                return len;
            }
        }
        return maxCount;
    }
}

---

输出