🌕 🌗 201. 数字范围按位与

难度: 🌕 🌗

问题描述

---

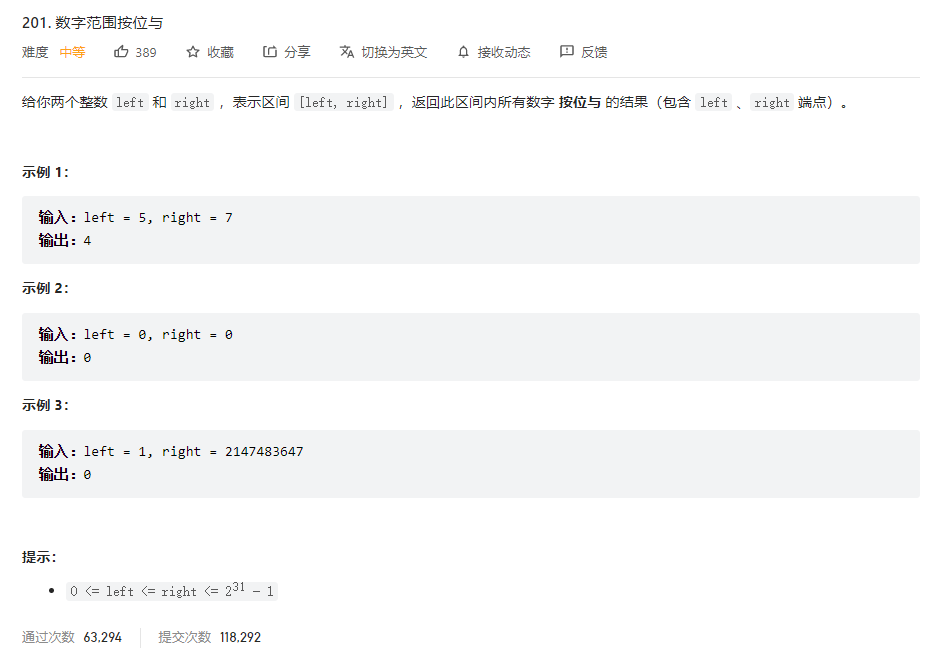
解法 1

class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        // 思路：
        // 因为是所有元素按位相与，那么要使某一位 == 1，需保证该位所有元素均 == 1
        // 可以看出公式，假设某值 left : 二进制形式为 abcd 1efg 此时就考虑 e 前面的那个 1
        // 所在位数为 2^3，从右往左为低位到高位
        // 要保证 [left, right] 该位全 == 1，则 该位有 2^3 能出现 1
        // 而 left 不一定是出现 1 的起始位置，需要去除 left 左边的某些个出现 1 的个数
        // ∴ left 在内，往大了数，最多有 [2^ 3 - (left - 2^3)] = (2^4 - left & (2^4 - 1)) 个 1
        // ∴ 最大右边界 end - left + 1 = 2^4 - left & (2^4 - 1)
        // 整理得，end = 2^4 - 1 + left => 即 left 所在 1 的位左移一位得到的值 - 1
        if(left == 0) {
            return 0; // 任何位 & 0 == 0
        }
        int res = 0;
        for(int i = 0; i < 32; i ++) {
            int cur = (1 << i);
            // System.out.println(cur);
            if((left & cur) > 0) {
                // 判断该位直到right 能否保留，即求 最大能到达的右边界 end
                int end = (cur << 1) - 1 - (left & ((cur << 1) - 1)) + left;
                // System.out.println(cur + "  " + end);
                if(right <= end) {
                    // 能够保留
                    res = res | cur;
                }
            } 
        }
        return res;
    }
}

---

输出 1

---

解法 2 - 另一种方法

class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        // 思路：
        // 找 left & right 的最长公共前缀，一直右移，直到 两数相等
        int exp = 0;
        while(left != right) {
            left >>>= 1;
            right >>>= 1;
            exp ++;
        }
        // 这样就保证了低位不相等的位全部屏蔽
        return left << exp;
    }
}

---

输出