🌗 223. 矩形面积

难度: 🌗

问题描述

---

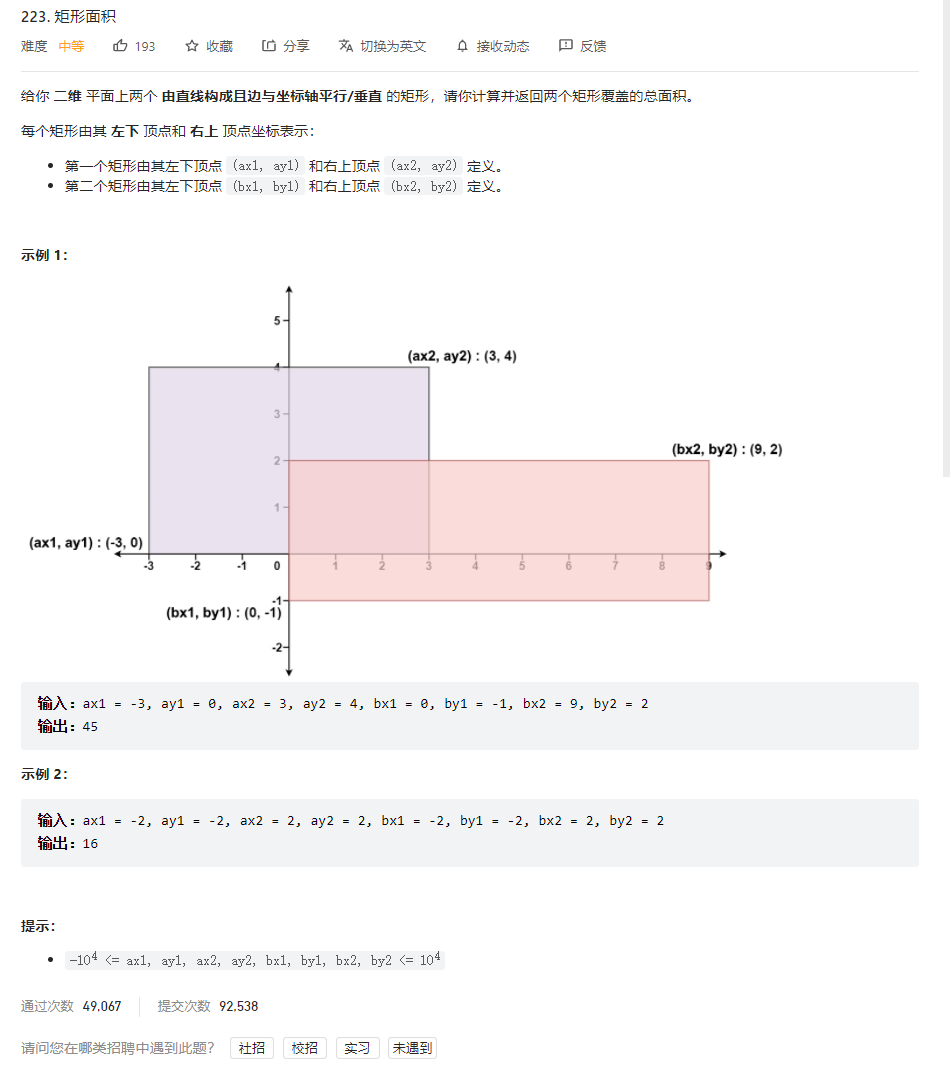
解法

class Solution {
    int max = Integer.MAX_VALUE;
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        // 思路：
        // 覆盖区域也是一个矩形，需要确定新矩形的四条边
        // 以横坐标为例，确定横轴 2 个端点
        int area = (ax2 - ax1) * (ay2 - ay1) + (bx2 - bx1) * (by2 - by1);
        int[] x = mySol(ax1, ax2, bx1, bx2);
        if(x[0] == max) {
            return area;
        }
        int[] y = mySol(ay1, ay2, by1, by2);
        if(y[0] == max) {
            return area;
        }
        return area - (x[1] - x[0]) * (y[1] - y[0]);
    }

    private int[] mySol(int m, int n, int p, int q) {
        int[] res = new int[]{max, max};
        // [m, n] & [p, q] 求覆盖区域
        int wm = n - m;
        int wp = q - p;
        if(wm > wp) {
            // 交换点，始终保持 [m, n] 的区域最小
            int tmp = m;
            m = p;
            p = tmp;
            tmp = n;
            n = q;
            q = tmp;
        }
        // System.out.println(m + "  " + n + "  " + p  + "  " + q);
        if(q <= m || p >= n) {
            return res;
        }
        // 存在重合区域
        if(p <= m && q >= n) {
            res[0] = m;
            res[1] = n;
            return res; // [p, q] 完全包裹 [m, n]
        }
        if(p >= m && p <= n) {
            res[0] = p;
            res[1] = n;
            return res;
        }
        if(q >= m && q <= n) {
            res[0] = m;
            res[1] = q;
            return res;
        }
        return res;
    }
}

---

输出