🌕🌕 390. 消除游戏

难度: 🌕🌕

问题描述

---

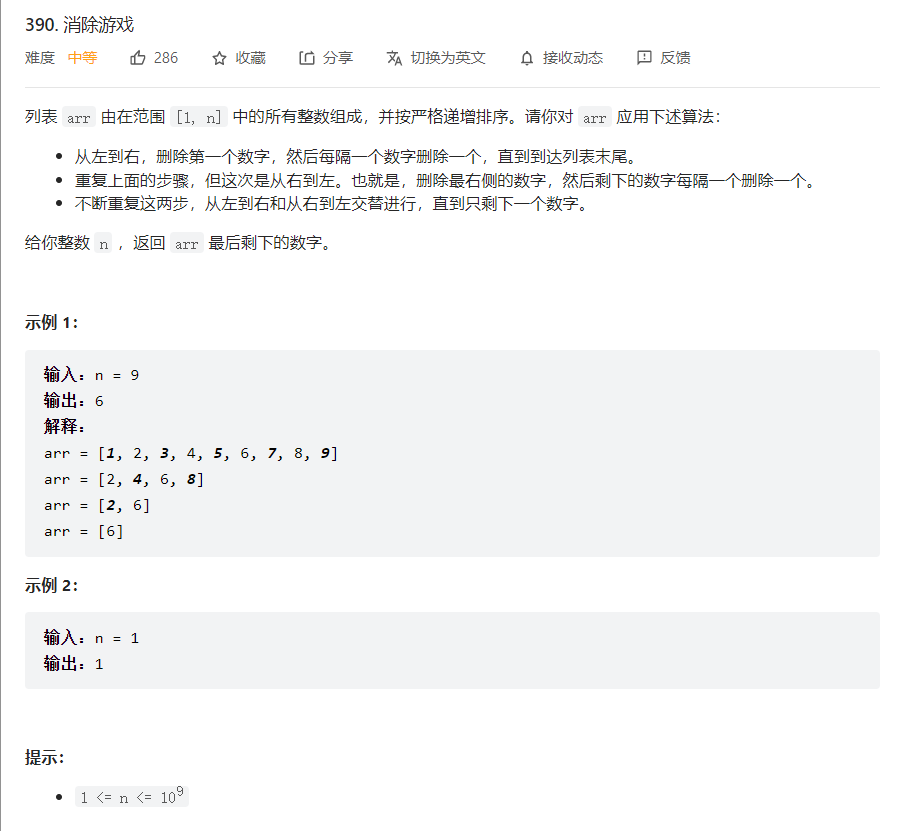
解法

class Solution {
    int end;
    public int lastRemaining(int n) {
        // 思路：
        // 假设 n = 16 | 14 两种情况
        // 0 - step = 1: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
        // 1 - step = 2: [2, 4, 6, 8, 10, 12, 14, 16] 
        // 2 - step = 4: [2, 6, 8, 10] | [4, 8, 12]
        // 3 - step = 8: [6, 10] | [8]
        // 4 - step = 16: [6] | [8]
        // 可以看出：
        // 1. 每次变化后，步长为 2 的幂 指数级增长
        // 2. 从左到右时，首个值肯定不能保留
        // 3. 从右到左时，需要根据 步长 & 末端点值判断是否保留首个数，末端点值可以根据首个值 & 步长得到
        // 4. 因此每轮只需要记录 当前是第几轮就可以得出为奇数轮还是偶数轮，以及 步长大小，再根据 首节点值就可得到下一轮状态
        end = n;
        return mySol(1, 0);
    }

    private int mySol(int left, int count) {
        int step = (int)Math.pow(2, count); // 当前轮步长
        // 递归终止条件
        if(left + step > end) {
            // 说明就剩这一个数了
            return left;
        }
        // left + step <= end 说明还需要再删除本轮里的数
        if((count & 1) == 0) {
            // count 为偶数，说明需要从左到右删除，首节点肯定保不住
            return mySol(left + step, count + 1);
        } else {
            // count 为奇数，需要从右到左删除，判断首节点是否会保留
            // 计算当前轮末尾节点值
            int curEnd = left + step * ((end - left) / step);
            // 用末尾节点值 / 当前步长，得出当前轮有奇数还是偶数个数
            int tmp = (curEnd - left) / step + 1;
            // 如果剩下奇数个数，从右到左删，会把首节点也删掉；若为偶数个数，删除的都是偶数下标，首节点保留
            if((tmp & 1) == 1) {
                return mySol(left + step, count + 1);
            } else {
                return mySol(left, count + 1);
            }
        }
    }
}

---

输出