🌕 🌗 60. 排列序列

难度: 🌕 🌗

问题描述

---

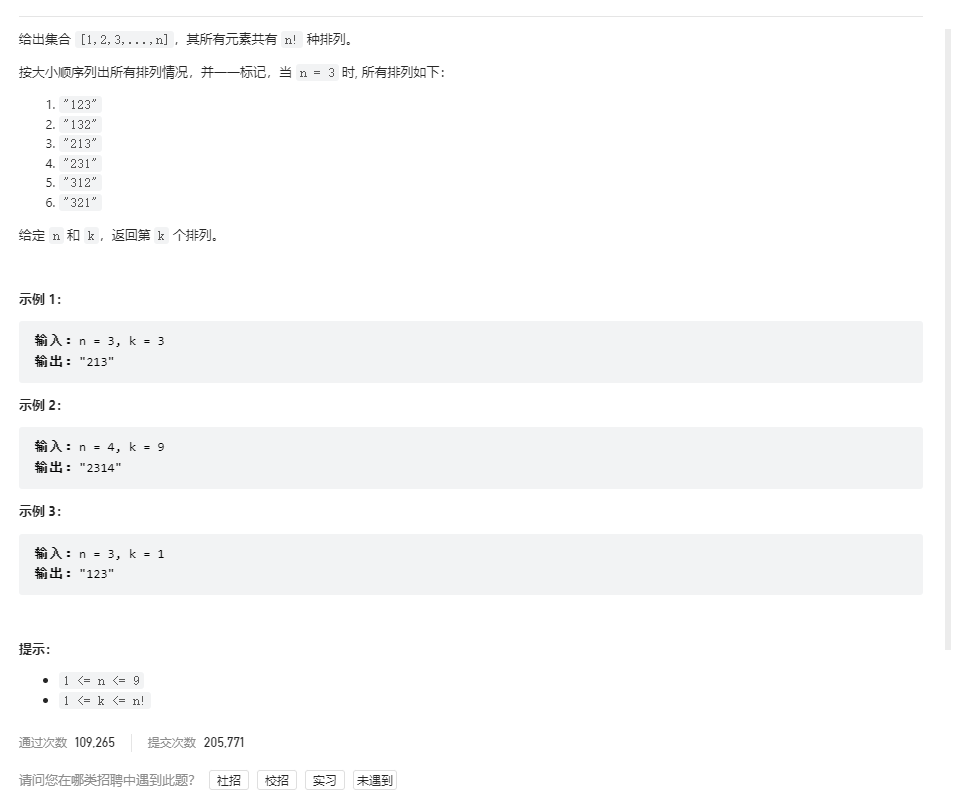
解法 1 - 回溯

class Solution {
    int count = 0;
    String res;
    public String getPermutation(int n, int k) {
        // 思路：
        // 回溯
        HashSet<Integer> set = new HashSet<>();
        LinkedList<Integer> path = new LinkedList<>();
        int[] dp = new int[n];
        if(n == 1) {
            return "1";
        }
        dp[1] = 1;
        for(int i = 2; i < n; i ++) {
            dp[i] = dp[i - 1] * i;
        }
        if(k > dp[n - 1]) {
            int pre = k / dp[n - 1];
            int left = k % dp[n - 1];
            if(left > 0) {
                set.add(pre + 1);
                k -= dp[n - 1] * pre;
                path.addLast(pre + 1);
                mySol(n, k, set, path);
            } else {
                set.add(pre);
                path.addLast(pre);
                k -= dp[n - 1] * (pre - 1);
                mySol(n, k, set, path);
            }
        } else {
            set.add(1);
            path.add(1);
            mySol(n, k, set, path);
        }
        // mySol(n, k, set, path);
        return res;
    }

    private void mySol(int n, int target, HashSet<Integer> set, LinkedList<Integer> path) {
        // 递归终止条件
        if(path.size() == n) {
            count ++;
            if(count == target) {
                res = getRes(path);
            }
            return;
        }
        if(count >= target) {
            return;
        }
        // path.size() < n
        for(int i = 1; i <= n; i ++) {
            if(set.contains(i)) {
                continue;
            }
            path.addLast(i);
            set.add(i);
            mySol(n, target, set, path);
            set.remove(i);
            path.removeLast();
        }
    }

    private String getRes(LinkedList<Integer> path) {
        StringBuilder sb = new StringBuilder();
        int len = path.size();
        for(int i = 0; i < len; i ++) {
            sb.append(path.get(i));
        }
        return sb.toString();
    }
}

---

输出 1

---

解法 2 - 找规律

class Solution {
    int[] used;
    int len;
    public String getPermutation(int n, int k) {
        // 思路：
        // 找规律
        if(n == 1) {
            return "1";
        }
        if(k == 0) {
            StringBuilder sb = new StringBuilder();
            for(int i = 1; i <= n; i ++) {
                sb.append(i);
            }
            return sb.toString();
        }
        // n > 1 && k > 0
        len = n;
        used = new int[n + 1];
        int[] dp = new int[n];
        dp[1] = 1;
        for(int i = 2; i < n; i ++) {
            dp[i] = i * dp[i - 1];
        }
        // System.out.println(Arrays.toString(dp));
        int[] array = new int[n]; // 存放 k 可以拆分的个数
        int min = 0;
        for(int i = n - 1; i > 0; i --) {
            if(k >= dp[i]) {
                int tmp = k / dp[i];
                int left = k - tmp * dp[i];
                array[i] = tmp;
                k = left;
                if(k == 0) {
                    min = i;
                    break;
                }
            }
        }
        // System.out.println(Arrays.toString(array));
        StringBuilder s = new StringBuilder();
        // 根据 array[] 得到 res
        int index = n - 1;
        while(index >= min) {
            if(array[index] == 0) {
                s.append(getMax(1));
                index --;
            } else {
                break;
            }
        }
        // System.out.println(min  + "   " + index);
        
        while(index >= min) {
            if(index > min) {
                int cur = getMax(array[index] + 1);
                s.append(cur);
            } else {
                int cur = getMax(array[index]);
                s.append(cur);
                if(min > 1) {
                    for(int i = len; i > 0; i --) {
                        if(used[i] == 0) {
                            s.append(i);
                        }
                    }
                    return s.toString();
                }
            }
            index --;
        }
        // 把没有使用的数，按照从小到大依次填充
        for(int i = 1; i <= len; i ++) {
            if(used[i] == 0) {
                s.append(i);
            }
        }
        return s.toString();
    }

    private int getMax(int k) {
        // 返回 used[] 中第 k 大的数
        int count = 0;
        for(int i = 1; i <= len; i ++) {
            if(used[i] == 1) {
                continue;
            }
            count ++;
            if(count == k) {
                used[i] = 1;
                return i;
            }
        }
        return -1;
    }
}

---

输出 2