🌕 🌕 673. 最长递增子序列的个数

难度: 🌕 🌕

问题描述

---

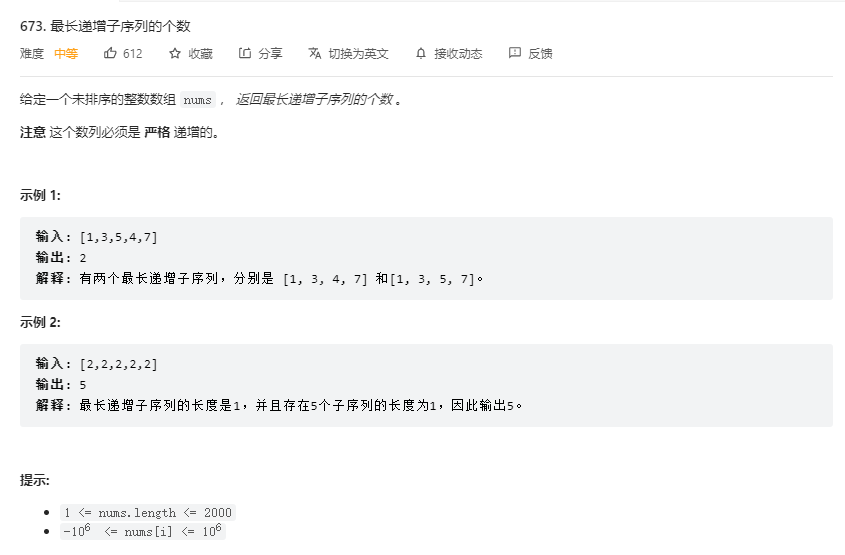
解法 1 - dp

class Solution {
    public int findNumberOfLIS(int[] nums) {
        // 思路：
        // dp 
        // 记录每个下标处的最长递增子序列的长度
        // 还要记录每个下标处的最长递增子序列的情况数
        int len = nums.length;
        int res = 0;
        int[] dp = new int[len];
        int[] count = new int[len];
        Arrays.fill(dp, 1);
        Arrays.fill(count, 1);
        for(int j = 1; j < len; j ++) {
            for(int i = 0; i < j; i ++) {
                if(nums[i] < nums[j]) {
                    // 以 dp[i] 为结尾下标的最长子序列 拼接 dp[j]
                    if(dp[i] + 1 > dp[j]) {
                        dp[j] = dp[i] + 1;
                        count[j] = count[i];
                    } else if(dp[i] + 1 == dp[j]) {
                        count[j] += count[i];
                    }
                }
            }
        }
        // 遍历 count[]
        int max = 0;
        for(int i = 0; i < len; i ++) {
            if(dp[i] > max) {
                max = dp[i]; // 之前从没出现过该长度的子序列
                res = count[i];
            } else if(dp[i] == max) {
                res += count[i];
            }
        }
        return res;
    }
}

---

输出 1

---

解法 2 - 借助二分

class Solution {
    public int findNumberOfLIS(int[] nums) {
        // 与 300 二分法类似
        // 区别在于，除了记录最新牌堆值，还需要记录所有牌堆值，这样可以遍历计算子序列的个数
        // 牌堆每个牌，需要同时记录其值 & 以该值为右边界的最长子序列个数
        int len = nums.length;
        List<int[]>[] top = new List[len];
        // 首先放入一张牌
        int[] first = new int[]{nums[0], 1};
        List<int[]> list = new ArrayList<>();
        list.add(first);
        top[0] = list;
        int end = 0;
        for(int i = 1; i < len; i ++) {
            int cur = nums[i];
            int index = mySol(top, 0, end, cur);
            if(index == end + 1) {
                // 新建牌堆
                end ++;
                top[index] = new ArrayList<int[]>();
            }
            int[] tmp = new int[]{cur, 0};
            if(index == 0) {
                // 当前值属于第一牌堆，长度为1的子序列且以该值为右边界，那么只有一种情况
                tmp[1] = 1;
            } else {
                // 统计 index - 1 长度的子序列 拼接 nums[i] 可以有多少种情况
                List<int[]> preList = top[index - 1];
                int size = preList.size();
                for(int j = 0; j < size; j ++) {
                    int[] preCur = preList.get(j);
                    if(cur > preCur[0]) {
                        // 可以进行拼接
                        tmp[1] += preCur[1];
                    }
                }
            }
            List<int[]> curList = top[index];
            // System.out.println(nums[i] + "   " + index + "   " + Arrays.toString(tmp));
            curList.add(tmp);
            top[index] = curList;
        }
        // 最后一个牌堆为最长子序列
        List<int[]> finalList = top[end];
        int res = 0;
        for(int i = 0; i < finalList.size(); i ++) {
            res += finalList.get(i)[1];
        }
        return res;
    }

    private int mySol(List<int[]>[] top, int left, int right, int target) {
        List<int[]> list = top[left];
        int size = list.size();
        // 特殊情况特判
        if(target <= list.get(size - 1)[0]) {
            return left;
        }
        list = top[right];
        size = list.size();
        if(target > list.get(size - 1)[0]) {
            return right + 1;
        }
        // target > [left] && target < [right]
        int mid = left + ((right - left) >> 1);
        list = top[mid];
        size = list.size();
        int cur = list.get(size - 1)[0];
        if(target == cur) {
            return mid;
        } else if(target > cur) {
            left = mid + 1;
            return mySol(top, left, right, target);
        } else {
            right = mid;
            return mySol(top, left, right, target);
        }
    }
}

---

输出 2

---

画图说明

原始输入数组

排成牌堆的结果，上面的值表示值，下面的值表示以该值为右边界形成的最长严格递增子序列的情况数

当 300 题中只需要一个最长子序列结果时，只需要维护每一列链表的尾节点作为新节点即可，而无需维护链表前面的节点值