🌕 🌗 45. 跳跃游戏 II

难度: 🌕 🌗

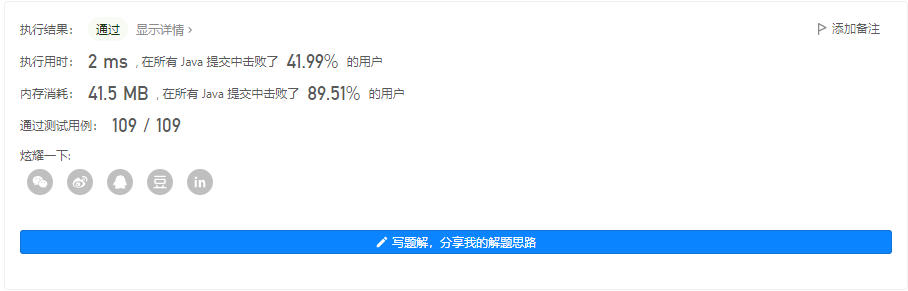
问题描述

---

解法 1

class Solution {
    public int jump(int[] nums) {
        // 思路：
        // dp[i]
        int len = nums.length;
        if(len == 1) {
            return 0;
        }
        int[] dp = new int[len];
        Arrays.fill(dp, len);
        dp[0] = 0;
        for(int i = 0; i < len; i ++) {
            int maxIndex = i + nums[i];
            if(maxIndex >= len - 1) {
                return dp[i] + 1;
            }
            for(int j = i + 1; j <= maxIndex; j ++) {
                dp[j] = Math.min(dp[j], dp[i] + 1);
            }
        }
        return dp[len - 1];
    }
}

---

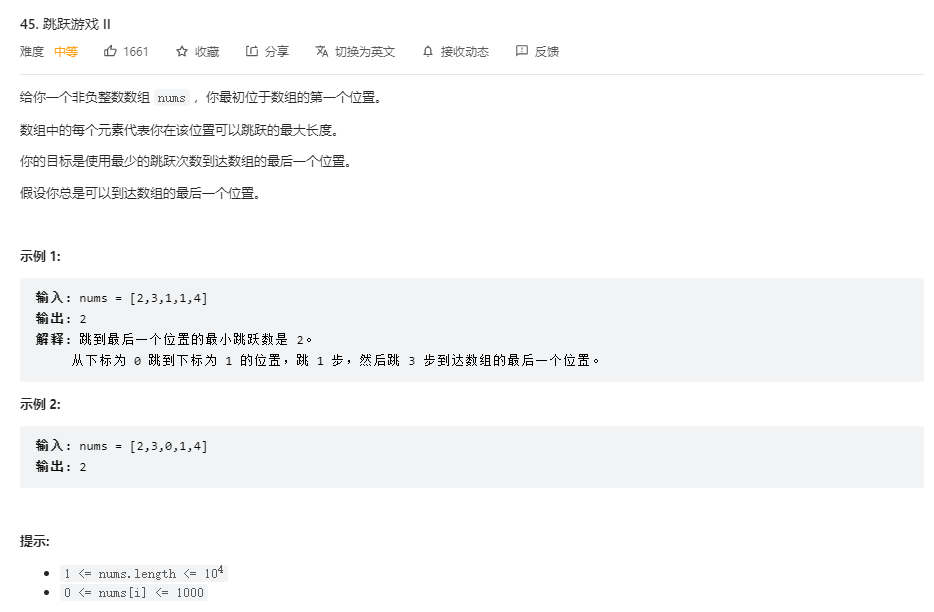
输出 1

---

解法 2 - 换种思路优化

class Solution {
    public int jump(int[] nums) {
        // 思路：
        // 贪心算法
        // 每次更新从当前节点出发能够到达的最远距离
        // 记录上次更新步数时，能到达的最远距离，达到边界，则需要增加步数
        int len = nums.length;
        if(len == 1) {
            return 0;
        }
        int[] dp = new int[len]; // 在 i 处能够到达的最远距离
        int res = 0; // 初始需要跳 0 步
        int end = 0; // 上次更新跳跃次数，能够到达的最远距离，超过则需要增加步数

        for(int i = 0; i < len; i ++) {
            int curMax = nums[i] + i; // 从当前位置出发，能到达的最远距离
            if(i > 0) {
                dp[i] = Math.max(dp[i - 1], curMax);
            } else {
                dp[i] = curMax;
            }

            if(dp[i] >= len - 1) {
                return res + 1;
            }

            // 判断是否需要更新跳跃次数
            if(i == end) {
                res ++;
                end = dp[i];
            }
        }
        return res;
    }
}

---

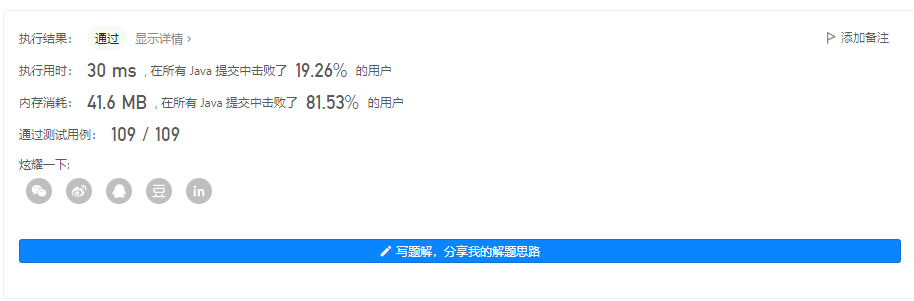
输出