🌕🌕 410. 分割数组的最大值

难度: 🌕🌕

问题描述

---

解法 1 - dp

class Solution {
    public int splitArray(int[] nums, int m) {
        // 思路：
        // dp[i][j] -- 以 [0, i] 划分为 j 段 得到的子数组的和的最大值的 最小
        // dp[i][j] = min{dp[i][j], max{dp[k][j - 1], sum[k + 1, len - 1]}}
        int len = nums.length;
        if(len == 1) {
            return nums[0];
        }
        int[][] dp = new int[len][len + 1];
        for(int i = 0; i < len; i ++) {
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        // 初始化 - 单个元素只能划分为 1 段
        int[] arr = new int[len]; // 前缀和数组
        arr[0] = nums[0];
        dp[0][1] = arr[0];
        for(int i = 1; i < len; i ++) {
            arr[i] = arr[i - 1] + nums[i];
            dp[i][1] = arr[i];
        }
        // dp
        for(int i = 1; i < len; i ++) {
            for(int j = 2; j <= Math.min(i + 1, m); j ++) {
                // [0, i] 中遍历找分割点 k
                for(int k = 0; k <= i; k ++) {
                    dp[i][j] = Math.min(dp[i][j], Math.max(dp[k][j - 1], arr[i] - arr[k]));
                }
            }
        }
        return dp[len - 1][m];
    }
}

---

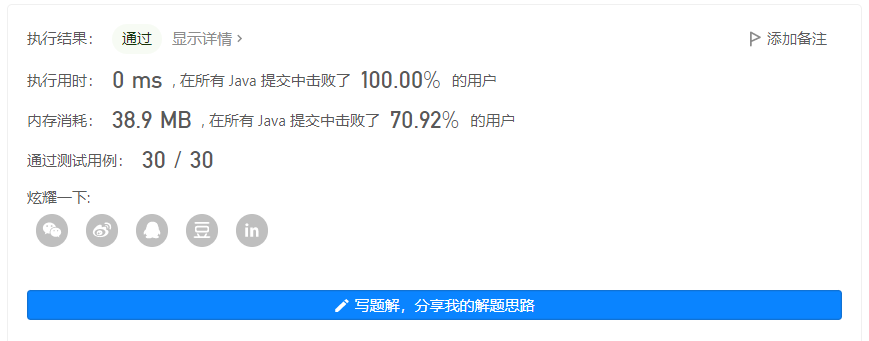
输出 1

---

解法 2 - 二分 + 贪心

class Solution {
    public int splitArray(int[] nums, int m) {
        // 思路：
        // 将整个数组划分为多个子数组，那么子数组的和 ∈ [max, sum]
        // max 为数组中最大的那个元素值，因为这个元素比存在于某个子数组中
        // sum 为数组元素总和
        // sum 只要数组不变，那么 sum 也为恒定值
        // 尝试在 [max, sum] 间找到一个值，设为 mid，将这个值作为所有子数组和的最大值的最小值，即目标值
        // 然后判断能否在该目标下，将数组划分为 m 个子数组
        // 如果满足，减小 mid，继续查找
        // 如果不满足，增大 mid，继续查找
        // 这就是 二分
        int len = nums.length;
        if(len == 1) {
            return nums[0];
        }
        int max = nums[0];
        int sum = 0;
        // 遍历，得到 max & sum
        for(int i = 0; i < len; i ++) {
            max = Math.max(max, nums[i]);
            sum += nums[i];
        }
        // 确定 max & sum 后，找中点，判断能否将其划分为 m 个子数组
        int left = max;
        int right = sum;
        while(left < right) {
            int mid = left + ((right - left) >> 1);
            if(isValid(nums, m, mid)) {
                // 可以将 nums 划分为 m 个子数组，子数组最大和均 <= mid，缩小 mid
                right = mid;
            } else {
                // 不可以划分为 m 个子数组，增大 mid
                left = mid + 1;
            }
        }
        return left;
    }

    private boolean isValid(int[] nums, int m, int target) {
        int prev = 0;
        int count = 1; // 要使得每个子数组的和均小于 target，nums 至少需要被分成 count 个数组
        for(int i = 0; i < nums.length; i ++) {
            if(prev + nums[i] <= target) {
                prev += nums[i]; // 无需再次分为子数组
            } else {
                // 当前值需要划分到一个新的数组里面
                prev = nums[i];
                count ++;
            }
        }
        return count <= m;
    }
}

---

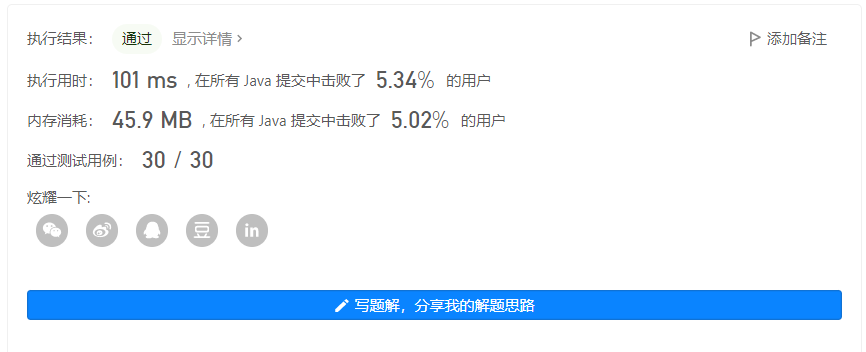
输出 2