🌕🌕 354. 俄罗斯套娃信封问题

难度: 🌕🌕

问题描述

---

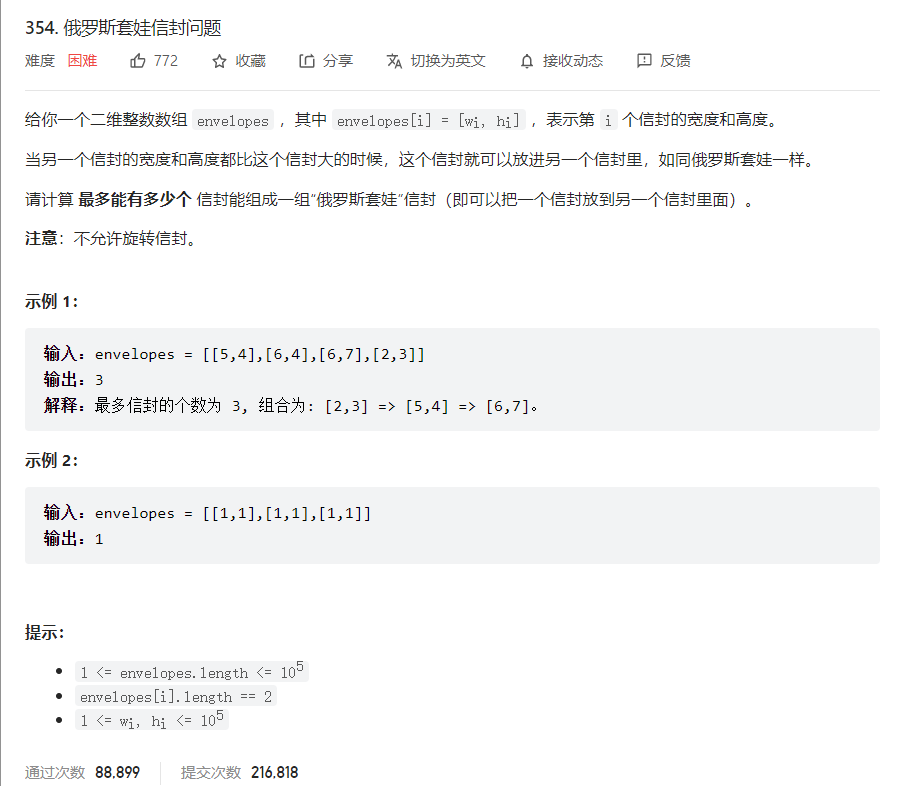
解法 1 - dp 超时

class Solution {
    public int maxEnvelopes(int[][] envelopes) {
        // 思路：
        // 排序 + dp
        // 首先将信封根据 任一维度排序，假设根据 宽度升序，高度无所谓
        // 转换为 在 [0, n] 中最多取 x 个信封满足 套娃条件
        // dp 问题 dp[i] = Math.max(dp[i], dp[j] + 1)
        int len = envelopes.length;
        Arrays.sort(envelopes, (a, b) -> {
            return a[0] - b[0];
        });
        int[] dp = new int[len];
        Arrays.fill(dp, 1);
        int res = 1;

        for(int i = 1; i < len; i ++) {
            // i 表示当前 i 信封被选中
            for(int j = 0; j < i; j ++) {
                // j 表示 i 前面的信封 j 被选中
                if(envelopes[i][1] > envelopes[j][1] && envelopes[i][0] > envelopes[j][0]) {
                    // 信封 j 的宽 & 高均满足条件
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                    res = Math.max(res, dp[i]);
                }
            }
        }
        return res;
    }
}

---

解法 2 - 300

class Solution {
    public int maxEnvelopes(int[][] envelopes) {
        // 思路：
        // 还是先排序，根据任一维度排序，假设为宽度升序
        // 题意转换为 在数组中宽度升序，从高度中选取最长递增子序列，求最长递增子序列的长度
        // 高度升序 还是 降序 对结果是否有影响？
        // 1) 假设 高度升序，那么同一宽度下选取了某高度值 x 满足条件
        // 然后再次选取了后面的同一宽度下的某高度值 y，x < y 自动成立，此时同一宽度选取 2 个信封，不满足题意
        // 2) 假设 高度降序，那么同一宽度下选取了某高度值 x 满足条件
        // 然后不可能再次选取后面的同一宽度下的某高度值 y，只能要么选 x 要么选 y，从而保证同一宽度最多同时选取一个信封
        int len = envelopes.length;
        Arrays.sort(envelopes, (a, b) -> {
            if(a[0] == b[0]) {
                return b[1] - a[1];
            } else {
                return a[0] - b[0];
            }
        });

        int count = 1;
        int[] arr = new int[len]; // 牌堆
        arr[0] = envelopes[0][1]; // 排序后只剩高度值有效
        for(int i = 1; i < len; i ++) {
            int cur = envelopes[i][1];
            // 特殊情况特判
            if(cur <= arr[0]) {
                arr[0] = cur;
                continue;
            }
            if(cur > arr[count - 1]) {
                count ++;
                arr[count - 1] = cur;
                continue; // 新建牌堆
            }
            // 二分查找当前牌的插入位置
            int index = mySol(arr, cur, 0, count - 1);
            arr[index] = cur;
        }
        return count;
    }

    private int mySol(int[] arr, int cur, int left, int right) {
        // 递归终止条件
        if(left >= right) {
            return left;
        }
        if(cur <= arr[left]) {
            return left;
        }
        if(cur > arr[right]) {
            return right + 1;
        }
        int mid = left + ((right - left) >> 1);
        if(cur == arr[mid]) {
            return mid;
        } else if(cur < arr[mid]) {
            return mySol(arr, cur, left, mid);
        } else {
            // cur > arr[mid]
            return mySol(arr, cur, mid + 1, right);
        }
    }
}

---

输出 2