🌕🌕 395. 至少有 K 个重复字符的最长子串

难度: 🌕🌕

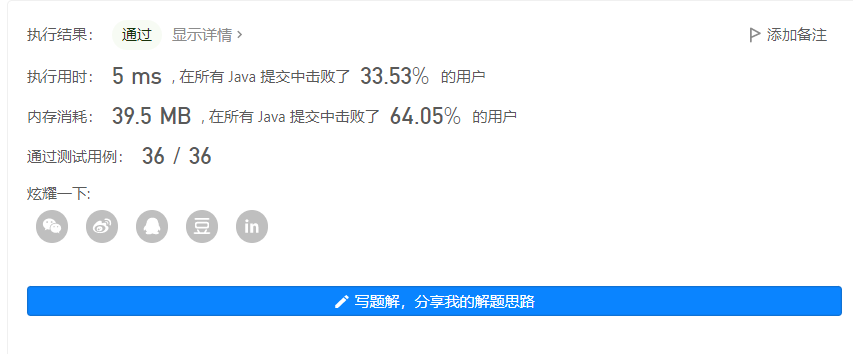
问题描述

---

解法 1 - 递归

class Solution {
    public int longestSubstring(String s, int k) {
        // 思路：
        // 将 s 分解成小字符串
        // 遍历 s，找到统计所有字符各自出现次数，如果某个字符 x 出现次数小于 k，说明包含 x 的字符串均无效
        // 因此可以以 x 为单位，将 s 切分成一个个不包含 x 的小字符串数组
        // 遍历小字符串数组中的每个小字符串，再次统计该小字符串中所有字符各自出现次数，...，以此递归
        return mySol(s, k);
    }

    private int mySol(String str, int k) {
        // 递归终止条件
        int len = str.length();
        if(k > len) {
            return 0;
        }
        // k <= len
        // 统计所有字符出现次数
        int[] arr = new int[26];
        for(char c: str.toCharArray()) {
            int index = c - 'a';
            arr[index] ++;
        }
        // 找出不满足 k 次的字符
        int res = len; // 如果不存在不满足 k 次的字符，说明整个字符串有效
        for(int i = 0; i < 26; i ++) {
            if(arr[i] != 0 && arr[i] < k) {
                char c = (char)(i + 'a');
                // 以 c 进行拆分
                int tmp = 0;
                String[] num = str.split("" + c);
                for(String cur: num) {
                    tmp = Math.max(tmp, mySol(cur, k));
                }
                return tmp; // 找到一个不满足条件的就切分，得到结果直接返回，而无需再次寻找其他不满足条件的字符进行切分
            }
        }
        return res;
    }
}

---

输出 1

---

解法 2 - 滑动窗口

class Solution {
    public int longestSubstring(String s, int k) {
        // 思路：
        // 如果是单纯的滑动窗口，假设当前时刻下满足要求，向右添加一个元素后，不满足要求，那么此时，指针如何滑动的不确定的
        // 假设向左滑动，需要去掉左边界所在字符和减去次数
        // 假设向右滑动，无法保证向右之后能满足右边界的元素达到次数，且整体满足条件；当然也无法保证一定无法满足条件
        // 因此，这样是无法进行窗口滑动的

        // 而如果在一个大前提下，即，固定当前滑动窗口中能够出现字符的种类数，再进行滑动
        // 假设当前时刻下满足要求，向右添加一个元素后：
        // 如果元素在种类数范围内，向右滑动窗口
        // 若元素添加后超出种类数范围，向左滑动窗口
        // 从而保证了窗口滑动的确定性
        int len = s.length();
        int res = 0;
        // 只有 26 个小写字母，因此字符种类数∈[1, 26]
        for(int var = 1; var <= 26; var ++) {
            // 统计只能出现 var 种字符的情况下，满足条件的最长字串长度
            int count = 0; // 当前字符总数
            int qualCount = 0; // 满足出现次数达到 k 次的字符总数
            int[] arr = new int[26]; // 存放每个字符的出现次数
            int i = 0;
            int j = 0; // 左右指针
            while(i <= j && j < len) {
                char c = s.charAt(j);
                int index = c - 'a';
                arr[index] ++;
                // 判断是否需要更新 count & qualCount
                if(arr[index] == 1) {
                    count ++; // 只有从 0 - 1 时更细
                }
                if(arr[index] == k) {
                    qualCount ++;
                }
                // 每次向右添加一个字符后，判断当前窗口是否满足条件
                // 如果不满足，需要缩减左窗口
                while(count > var) {
                    char left = s.charAt(i);
                    int tmpIndex = left - 'a';
                    if(arr[tmpIndex] == k) {
                        qualCount --;
                    }
                    if(arr[tmpIndex] == 1) {
                        count --;
                    }
                    arr[tmpIndex] --;
                    i ++;
                }
                // 种类数满足要求，判断是否所有字符均达到 k 次
                if(count == qualCount) {
                    res = Math.max(res, j - i + 1);
                }
                j ++;
            }
        }
        return res;
    }
}

---

输出 2