🌕🌕 785. 判断二分图

难度: 🌕🌕

问题描述

---

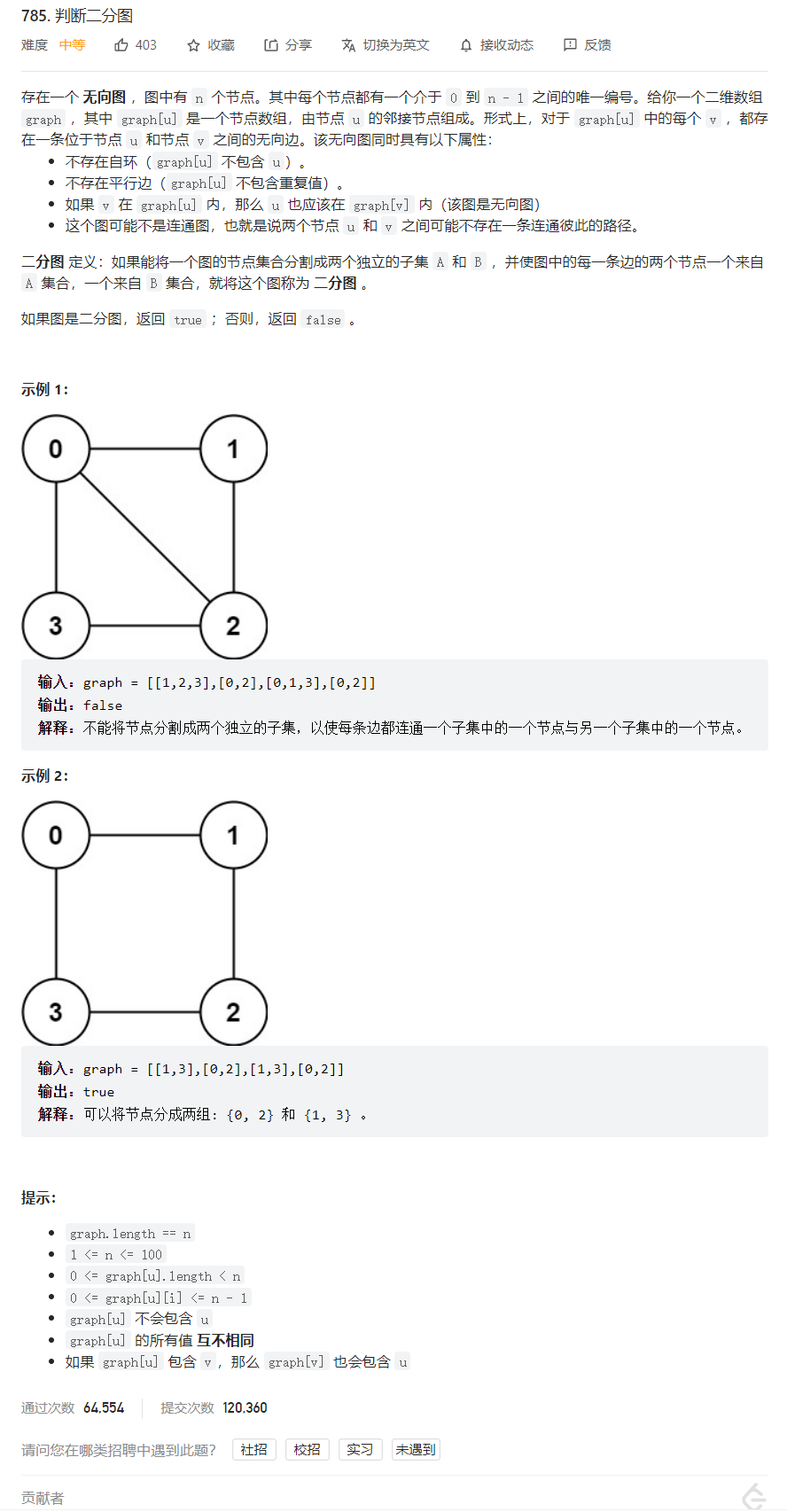
解法 1 - dfs

class Solution {
    public boolean isBipartite(int[][] graph) {
        // 思路：
        // 染色，对于当前节点，它周围的颜色均和它不同，最后成功分成 两部分颜色
        // dfs
        int len = graph.length;
        int[] visited = new int[len];
        // 不可只从 首节点 进行染色，染色完成后，需保证所有节点均被遍历到，均染过色
        for(int i = 0; i < len; i ++) {
            if(visited[i] == 0) {
                if(!mySol(graph, visited, i, 1)) {
                    return false;
                }
            }
        }
        return true;
    }

    private boolean mySol(int[][] graph, int[] visited, int index, int exp) {
        // 递归终止条件
        if(visited[index] != 0) {
            if(visited[index] != exp) {
                return false;
            } else {
                return true;
            }
        }
        // [index] == 0 需要染色
        visited[index] = exp;
        // 遍历其所有相邻节点，染 相反色
        int[] arr = graph[index];
        if(exp > 0) {
            exp = -1;
        } else {
            exp = 1;
        }
        for(int i: arr) {
            if(!mySol(graph, visited, i, exp)) {
                return false;
            }
        }
        return true;
    }
}

---

输出 1

---

解法 2 - bfs

class Solution {
    public boolean isBipartite(int[][] graph) {
        // 思路：
        // bfs - 染色
        int len = graph.length;
        int[] visited = new int[len];
        LinkedList<Integer> queue = new LinkedList<>();
        // 遍历的是 节点下标，因为下标是有序的，可保证所有节点都会入队过
        for(int i = 0; i < len; i ++) {
            if(visited[i] != 0) {
                // 说明已经遍历过，返回
                continue;
            }
            // [i] == 0 未被染色
            visited[i] = 1; // 染色
            // 该节点入队
            queue.offer(i);
            // bfs 遍历
            while(!queue.isEmpty()) {
                int cur = queue.poll(); // 正向队营
                // 找到相邻节点，全部为 反向队营
                int[] arr = graph[cur];
                // 遍历反向队营
                for(int j: arr) {
                    if(visited[j] > 0) {
                        return false;
                    }
                    visited[j] = -1;
                    // 反向队营的相邻节点均为 正向队营，入队
                    int[] fur = graph[j];
                    for(int k : fur) {
                        if(visited[k] < 0) {
                            return false;
                        } else if(visited[k] > 0) {
                            continue;
                        } else {
                            visited[k] = 1;
                            queue.offer(k);
                        }
                    }
                }
            }
        }
        return true;
    }
}

---

输出 2

---

解法 3 - 并查集

class Solution {
    int[] parent; // 每个下标处的父节点下标
    public boolean isBipartite(int[][] graph) {
        // 思路：
        // 并查集 - 最终应该被分成 2 部分
        int len = graph.length;
        parent = new int[len];
        // parent 初始化，每个下标的父节点都是自己
        for(int i = 0; i < len; i ++) {
            parent[i] = i;
        }
        // 遍历所有节点
        for(int i = 0; i < len; i ++) {
            int curFather = getFather(i);
            int[] arr = graph[i]; // 当前节点的相邻节点集合，它们应该处于同一父节点下，且和当前节点不在同一集合
            for(int j: arr) {
                int tmpFather = getFather(j);
                if(tmpFather == curFather) {
                    // 处于同一集合
                    return false;
                }
                // 将相邻节点连接
                union(arr[0], j);
            }
        }
        return true;
    }

    private void union(int i, int j) {
        int fa1 = getFather(i);
        int fa2 = getFather(j);
        parent[fa1] = fa2;
    }

    private int getFather(int index) {
        // 递归终止条件
        if(parent[index] == index) {
            return index;
        } else {
            return getFather(parent[index]);
        }
    }
}

---

输出 3